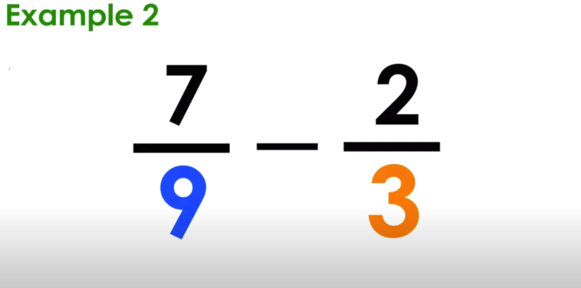How to Add and Subtract Fractions (Step-by-Step)

How to Add and Subtract Fractions Explained!

How can you add and subtract fractions with different denominators?

Welcome to this free lesson guide that accompanies this Adding and Subtracting Denominators with Unlike Denominators video lesson, where you will learn how to add and subtract fractions:

• Adding Fractions

• Subtracting Fractions

• Unlike Denominators

• How to add and subtract fractions with the same denominator

• How to add and subtract fractions with different denominators

This How to Add and Subtract Fractions with Unlike Denominators: Complete Guide includes several examples, a step-by-step tutorial, an animated video mini-lesson, and a free worksheet and answer key.

---

*This lesson guide accompanies our animated Adding and Subtracting Fractions with Unlike Denominators on YouTube.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Before you learn how to add and subtract fractions you need to understand some key vocabulary first.

Adding and Subtracting Fractions with the Same Denominator

Let’s start by reviewing the difference between a numerator and a denominator:

How to Add and Subtract Fractions with Like Denominators

In the above example, 1/5 and 3/5 have common denominators (both equal 5). To add them together, you just have to add the numerators together and leave the denominator alone as follows:

Since 4/5 can not be simplified any further, you can conclude that:

1/5 + 3/5 = 4/5

But what about when the denominators are not the same?

Adding and Subtracting Fractions with Unlike Denominators

How do you add and subtract fractions when the denominators are different?

You can use the following 3-step process for adding and subtracting fractions (with and without common denominators).

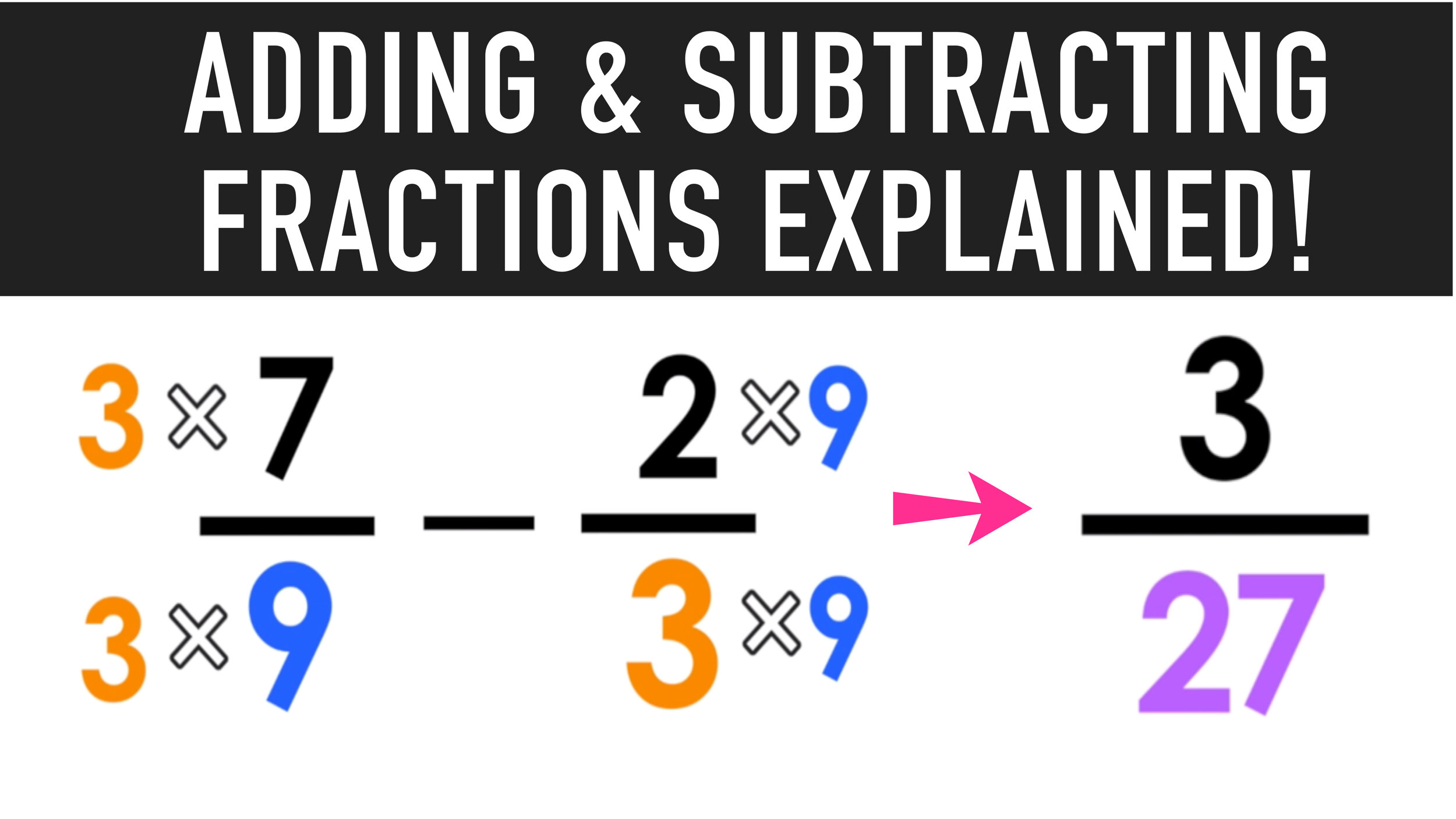
Subtracting Fractions with Unlike Denominators Example

STEP ONE: Get a common denominator.

How to add and subtract fractions.

STEP TWO: Add or subtract the numerators.

STEP THREE: Simplify the result if needed.

Notice that 3/27 can be simplified, since the numerator and denominator are both divisible by 3.

And that’s all there is to it!

Final Answer:

---

---

Adding and Subtracting Fractions with Unlike Denominators: Video Tutorial

Still confused? Check out the animated video lesson below:

Check out the video lesson below to learn more about adding and subtracting fractions and for more free practice problems:

---

---

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Geometry Transformations: Rotations 90, 180, 270, and 360 Degrees!

Performing Geometry Rotations: Your Complete Guide

The following step-by-step guide will show you how to perform geometry rotations of figures 90, 180, 270, and 360 degrees clockwise and counterclockwise and the definition of geometry rotations in math! (Free PDF Lesson Guide Included!)

Welcome to this free lesson guide that accompanies this Geometry Rotations Explained Video Tutorial where you will learn the answers to the following key questions and information:

• What is the geometry rotation definition and what is the definition of rotation in math?

• How to perform clockwise and counterclockwise rotations

• How can you rotate a triangle about the origin?

• Several geometry rotation examples

This Complete Guide to Geometry Rotations includes several examples, a step-by-step tutorial, a PDF lesson guide, and an animated video tutorial.

---

*This lesson guide accompanies our animated Geometry Transformations: Rotations Explained! video.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Rotation Geometry Definition

Before you learn how to perform rotations, let’s quickly review the definition of rotations in math terms.

Rotation Geometry Definition: A rotation is a change in orientation based on the following possible rotations:

• 90 degrees clockwise rotation

• 90 degrees counterclockwise rotation

• 180 degree rotation

• 270 degrees clockwise rotation

• 270 degrees counterclockwise rotation

• 360 degree rotation

Note that a geometry rotation does not result in a change or size and is not the same as a reflection!

Clockwise vs. Counterclockwise Rotations

There are two different directions of rotations, clockwise and counterclockwise:

Clockwise Rotations (CW) follow the path of the hands of a clock. These rotations are denoted by negative numbers.

Counterclockwise Rotations (CCW) follow the path in the opposite direction of the hands of a clock. These rotations are denoted by positive numbers.

Clockwise rotations are denoted by negative numbers.

Counterclockwise rotations are denoted by positive numbers.

Note that the direction of rotation (CW or CCW) doesn’t matter for 180 and 360-degree rotations, since they will both bring you to the same spot (more on this later).

Geometry Rotation Notation

Note that the following notation is used to show what kind of rotation is being performed.

For example, Figure 1 is a rotation of -270 degrees (which is a CW rotation).

Figure 1

Now you are ready to try a few geometry rotation examples!

---

---

Geometry Counterclockwise Rotation Examples

Example 01: 90 Degrees Counterclockwise About the Origin

Since 90 is positive, this will be a counterclockwise rotation.

In this example, you have to rotate Point C positive 90 degrees, which is a one quarter turn counterclockwise.

Point C lays in the 1st quadrant.

To perform the 90-degree counterclockwise rotation, imagine rotating the entire quadrant one-quarter turn in a counterclockwise direction.

Point C

Rotate the entire quadrant.

Plot point C’

Note the location of Point C’, the image of Point C after a 90-degree rotation.

And this process could be repeated if you wanted to rotation Point C 180 degrees or 270 degrees counterclockwise:

Point C after a 180-degree rotation.

Point C after a 270-degree rotation.

This example should help you to visually understand the concept of counterclockwise geometry rotations. Next, you will learn the rules for performing counterclockwise rotations.

>>> Before you move on, take some time to visualize what rotations look like on the coordinate plane.

<><><>

---

---

Counterclockwise Rotation Rules

You can use the following rules when performing any counterclockwise rotation.

By applying these rules to Point C (3,6) in the last example (Figure 2), you can see how applying the rule creates points that correspond with the graph!

Figure 2

These points should look familiar! They are the points that you plotted in the last example!

---

Geometry Clockwise Rotation Examples

Example 01: 90 Degrees Clockwise About the Origin

Since the rotation is 90 degrees, you will be rotating the point in a clockwise direction.

Now imagine rotating the entire 4th quadrant one-quarter turn in a clockwise direction:

Point D

Rotate the entire quadrant

Plot Point D’

Note the location of Point D’, the image of Point D after a -90-degree rotation.

And this process could be repeated if you wanted to rotation Point D -180 degrees or -270 degrees counterclockwise:

Point D after -180 rotation

Point D after -270 rotation

This example should help you to visually understand the concept of clockwise geometry rotations. Next, you will learn the rules for performing clockwise rotations.

>>> Before you move on, take some time to visualize what rotations look like on the coordinate plane.

<><><>

---

---

Clockwise Rotation Rules

You can use the following rules when performing any clockwise rotation.

By applying these rules to Point D (5,-8) in the last example (Figure 3), you can see how applying the rule creates points that correspond with the graph!

Figure 3

These points should look familiar! They are the points that you plotted in the last example!

---

More Geometry Rotations Examples

Example 01: Rotate a Line Segment 90 Degrees Clockwise

You can perform this rotation by using the rules or by doing a visual rotation as follows:

Example 02: Rotate a Triangle 180 Degrees

Note that it doesn’t matter which direction go (CW or CCW) for 180 degrees rotations, since you will end up in the same position either way!

You can perform this rotation by using the rules or by doing a visual rotation as follows:

---

Free Geometry Rotations Lesson Guide

Looking for more help with geometry rotations?

Click the link below to download your free PDF lesson guide that corresponds with the video lesson below!

Click here to download the Your Free PDF Lesson Guide

Still Confused?

Check out this animated video tutorial on geometry rotations:

---

---

Looking for more practice with Geometry Transformations?

Check out the following free resources:

Free Tutorial on Reflections!

Reflections Over the X- and Y-Axis: Complete Guide

Dilations and Scale Factor: Complete Guide

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Multiplying Polynomials: The Complete Guide

The Best Method for Multiplying Polynomials

The following step-by-step guide will show you how to multiply polynomials using the distributive method and includes 3 examples!

Welcome to this free lesson guide that accompanies this Multiplying Polynomials Made Easy! video tutorial where you will learn the answers to the following key questions and information:

• What is the best method for multiplying polynomials?

• How to perform multiplication of polynomials

• Multiplication of monomials, binomials, and trinomials

• Multiplying Polynomials Using the Distributive Property

This Complete Guide to Multiplying Polynomials includes several examples, a step-by-step tutorial and an animated video tutorial.

---

*This lesson guide accompanies our animated Multiplying Polynomials Made Easy! video.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Multiplying Polynomials Explained!

Before you learn how to multiply polynomials, let’s quickly review some important information:

The Distributive Property

Definition: The distributive property allows for you to multiply a sum by multiplying each term separately and then add all of the products together.

If you understand the distributive property, you will be able to multiply polynomials with ease.

Multiplying Polynomials Examples

Multiplying Polynomials Example 1: Multiplying by a Monomial

In this first example, you will be multiplying a monomial by a trinomial. You can think of this as multiplying one “thing” by “another thing” as follows:

This is where using the distributive property (or distributive method) will help you!

To multiply these polynomials, start by taking the first polynomial (the purple monomial) and multiplying it by each term in the second polynomial (the green trinomial).

This can be done by multiplying 4x^2 by the first term of the green trinomial (Figure 1), then by the second term of the green trinomial (Figure 2) and finally by the third term of the green trinomial (Figure 3).

Figure 1

Figure 2

Figure 3

The next step is to simplify each of these new terms and find their sum:

Simplify the first term.

Simplify the second term.

Simplify the third term.

The final step is to check and see if you can COMBINE LIKE TERMS. In this example, there are no like terms, so you can conclude that:

Final Answer:

Figure 2

---

Multiplying Polynomials Example 2: Multiplying Binomials

You can use the distributive method for multiplying polynomials just like the last example!

Start by multiplying the first term of the first binomial (3x) by the entire second binomial (Figure 1).

Then multiply the second term of the first binomial (-5y) by the entire second binomial (Figure 2).

Figure 1

Figure 2

The next step is to use the distributive property again to simplify each new term.

Note that you do not need the plus sign between -6xy and -40xy.

The final step is to COMBINE LIKE TERMS and simplify:

Final Answer:

---

---

Multiplying Polynomials Example 3: Multiply a Binomial by a Trinomial

Figure 1

Remember that you are still just multiplying two things together! And you can do that by using the distributive method again as follows:

Now you can use the distributive method again to simplify the new terms:

The final step is to COMBINE LIKE TERMS and simplify:

-42x^2 and -27x^2 combine to make -69x^2

+14x and +54x combine to make +68x

Now that you have combined like terms, you can conclude that:

Final Answer:

---

Still Confused?

Check out this animated video tutorial on multiplying polynomials:

---

---

Looking for more practice with multiplying polynomials?

Check out the following free resources:

Free Tutorial

Multiplying Binomials Using the Box Method: Complete Guide

Multiplying Binomials Using FOIL Method: Complete Guide

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Geometry Transformations: Dilations Made Easy!

Performing Geometry Dilations: Your Complete Guide

The following step-by-step guide will show you how to perform geometry dilations of figures and to understand dilation scale factor and the definition of geometry in math! (Free PDF Lesson Guide Included!)

Welcome to this free lesson guide that accompanies this Geometry Dilations Explained Video Tutorial where you will learn the answers to the following key questions and information:

• What is the geometry dilation definition and what is definition of dilation in math?

• What is a dilation scale factor?

• How can you dilate a figure like a triangle on the coordinate plane?

• Several dilation geometry examples

This Complete Guide to Geometry Dilations includes several examples, a step-by-step tutorial, a PDF lesson guide, and an animated video tutorial.

---

*This lesson guide accompanies our animated Geometry Transformations: Dilations Explained! video.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Dilation Geometry Definition

Before you learn how to perform dilations, let’s quickly review the definition of dilations in math terms.

Dilation Geometry Definition: A dilation is a proportional stretch or shrink of an image on the coordinate plane based on a scale factor.

• Stretch = Image Grows Larger

• Shrink = Image Grows Smaller

Note that a geometry dilation does not result in a change or orientation or shape!

Dilation Scale Factor

The following notation is used to denote dilations based on a scale factor of K:

K represents a number. When K=1 (the dilation scale factor is 1), the image does not change:

A scale factor one 1 is uncommon, because it doesn’t change anything!

But when K>1 (the dilation scale factor K is a number that is larger than 1), the image will be stretched!

If K=2, the image is stretched twice as large as the original!

And when K<1 (the dilation scale factor K is a number less than 1), the image will shrink. Note that the scale factor cannot be less than or equal to zero (this would completing eliminate the figure).

If K=1/2, the image shrinks to half of its original size.

When shrinking a figure, the scale factor is greater than zero, but less than one.

Now you are ready to try a few geometry dilation examples!

---

---

Geometry Dilation Examples

Example 1: Dilation Scale Factor >1

In this example, you have to dilate ▵OMG by a scale factor of 2 to create a new triangle: ▵O’M’G’.

Start by writing down the coordinates of the vertices of ▵OMG as follows:

The next step is to take the scale factor (2 in this example) and multiply it by the x and y-value of points O, M, and G, as follows:

Now you have the coordinates of O’, M’, and G’

You can now draw ▵O’M’G’ on the coordinate plane by plotting the points that you just found:

You have just constructed ▵O’M’G’, which is the image of ▵OMG after a dilation of 2.

<><><>

---

---

Example 2: Dilation Scale Factor <1

In this example, you have to dilate figure MASH by a scale factor of 1/3 to create a new figure: M’A’S’H’

Since the dilation scale factor is less than one, the new figure will be smaller version of the original (shrink).

Start by writing down the coordinates of the vertices of figure MASH as follows:

The next step is to take the scale factor (1/3 in this example) and multiply it by the x and y-value of points M, A, S, and H, as follows:

Now you have the coordinates of M’, A’, S’, and H’

You can now draw figure M’A’S’H’ on the coordinate plane by plotting the points that you just found:

You have just constructed M’A’S’H’, which is the image of MASH after a dilation of 1/3.

<><><>

---

Free Geometry Dilations Lesson Guide

Free PDF Lesson Guide

Looking for more help with geometry dilations?

Click the link below to download your free PDF lesson guide that corresponds with the video lesson below!

Click here to download the Your Free PDF Lesson Guide

Still Confused?

Check out this animated video tutorial on geometry dilations and scale factors:

---

---

Looking for more practice with Geometry Transformations?

Check out the following free resources:

Free Tutorial on Reflections!

Reflections Over the X- and Y-Axis: Complete Guide

Video Lessons:

Geometry Rotations Explained!

Geometry Translations Explained!

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Finding Slope of a Line: 3 Easy Steps

Finding Slope of a Line in y=mx+b Form: Everything You Need to Know

Are you ready to learn how to understand and identify the slope of a line and how to find the slope of a line?

Before you learn an easy method for finding slope (with and without a calculator), let’s make sure that you understand a few basics of slope, including the slope definition.

Slope Definition:

•  The slope of a line refers to its direction and steepness.

• There are 4 kinds of slope: positive, negative, zero, and undefined. In this guide, we are only going to look at positive and negative slope. Click here to watch a video tutorial review of the 4 kinds of slope.

Note that positive slopes increase from left to right and negative slopes decrease from left to right.

Finding Slope: Rise Over Run

The slope of a line is expressed as a fraction that is commonly referred to as rise over run.

The numerator (rise) refers to how many units up or down and the denominator (run) refers to how many units left or right. The direction will depend on whether or not the slope is positive or negative.

Positive Slope: Rise Over Run

Rise: UPWARDS Run: TO THE RIGHT

Negative Slope: Rise Over Run

Rise: DOWNWARDS Run: TO THE RIGHT

How to Find the Slope of a Line: 3 Easy Steps

You can find the slope of any line by following these three easy steps:

Step One: Determine if the slope if positive (increasing) or negative (decreasing)

Step Two: Using two points on the line, calculate the rise and the run and express it as a fraction (rise over run).

Step Three: Simplify the fraction if possible.

Let’s take a look at a few examples!

EXAMPLE: Find the slope of the line below.

Step One: Determine if the slope if positive (increasing) or negative (decreasing)

Notice that the line is increasing from left to right, so we know that this line has a positive slope!

Step Two: Using two points on the line, calculate the rise and the run and express it as a fraction (rise over run).

For this example, let’s start by choosing the left farthest point (-9,-6) and the right farthest point (9,6).

To find rise over run, draw a vertical line that rises from (-9,6) and a horizontal line that runs to (9,6), then count how many units you had to travel upward (rise) and how many to the right (run) and express it as a fraction as follows:

Rise over run is like building a staircase!

Step Three: Simplify the fraction if possible.

Right now, you can say that the slope of the line is 12/18. But 6/9 is also equivalent to 12/18, so let’s see what that would look like on the graph by starting from the first point (-9,-6) and this time rising up 6 and running to the right 9 units repeatedly as follows:

Notice how you end up in the same spot!

At this point, it is clear that the line has a slope of 12/18 and a slope of 6/9.

But we don’t want to have multiple slopes for the same line, so you will always express the slope of a line in simplest or reduced form.

In this example, the slopes of 12/18 and 6/9 can be simplified to 2/3 as follows:

And since 2/3 can not be simplified further, you can conclude that:

Final Answer: The line has a slope of positive 2/3

---

---

Finding Slope of a Line Examples

EXAMPLE #1: Find the Slope of the Line

View fullsize

Step One: Determine if the slope if positive (increasing) or negative (decreasing)

Notice that the line is increasing from left to right, so we know that this line has a positive slope!

Step Two: Using two points on the line, calculate the rise and the run and express it as a fraction (rise over run).

In this example, use the two given points as follows:

The rise is 6 and the run is 3.

Step Three: Simplify the fraction if possible.

You should know that 6/3 is equal to 2 (six divided by three). Since we want to think about slope as the fraction rise over run, we can express 2 as 2/1:

Notice that 6/3 reduces to 2/1 or just 2.

You can see that 2/1 is equivalent to 6/3 since the pink staircase on the graph above still gets you to the same point.

So now you can express your answer as follows:

Final Answer: The line has a slope of positive 2.

---

---

Finding Slope of a Line Examples

EXAMPLE #2: Find the Slope of the Line

Step One: Determine if the slope if positive (increasing) or negative (decreasing)

Notice that the line is decreasing from left to right, so we know that this line has a negative slope!

Step Two: Using two points on the line, calculate the rise and the run and express it as a fraction (rise over run). Remember that you have to rise down when dealing with negative slopes.

In this example, use the two given points as follows:

The slope is negative!

Step Three: Simplify the fraction if possible.

Notice that the fraction -3/8 can not be simplified further, so you can conclude that:

Final Answer: The line has a slope of - 3/8.

---

Looking to Learn More About Slope?

Check out these free video tutorials:

Free Slope Calculator

If you need a fast and easy way to find the slope of a line, then you can take advantage of the many free online slope calculators that are available.

This free slope calculator from calculator.net not only finds slope but it expresses it in reduced form and includes whether the slope is positive or negative.

To use the slope calculator, simply input the x and y-values for any two points on the line and press calculate.

Finding Slope of a Line Worksheet

Do you need more practice with finding the slope of a line? The following finding slope worksheet and answer key will give you plenty of opportunities to practice using the three-step process!

Click here to download your free Finding Slope Worksheet with Answers.

And if you are looking for a more in-depth lesson on how to find the slope of a line, check out this free Finding Slope Video Lesson:

Read More Posts About Math Education:

---

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.