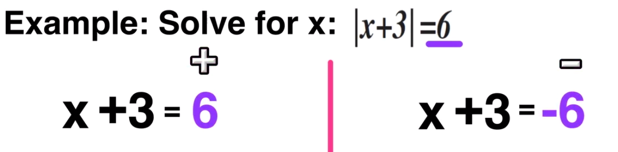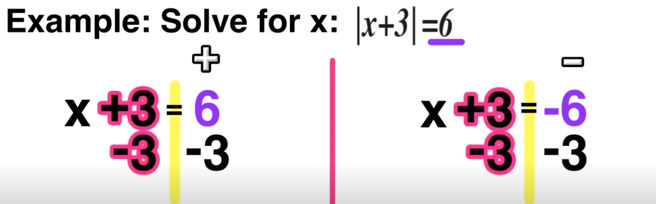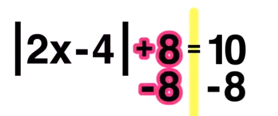Finding Slopes of Parallel and Perpendicular Lines (and Graphing): Complete Guide
The following step-by-step guide will show you how to use parallel slope and perpendicular slope to graph parallel and perpendicular lines
Welcome to this free lesson guide that accompanies this Graphing Parallel and Perpendicular Lines Using Slope Tutorial where you will learn the answers to the following key questions and information:
What is parallel slope?
What is perpendicular slope?
How can I graph parallel lines?
How can I graph perpendicular lines?
This Complete Guide to Parallel and Perpendicular Lines and Slope includes several examples, a step-by-step tutorial and an animated video tutorial.
*This lesson guide accompanies our animated Graphing Parallel and Perpendicular Lines Using Slope video.
Want more free math lesson guides and videos? Subscribe to our channel for free!
Parallel Slope and Perpendicular Slope
Before you learn how to graph parallel and perpendicular lines, let’s quickly review some important information:
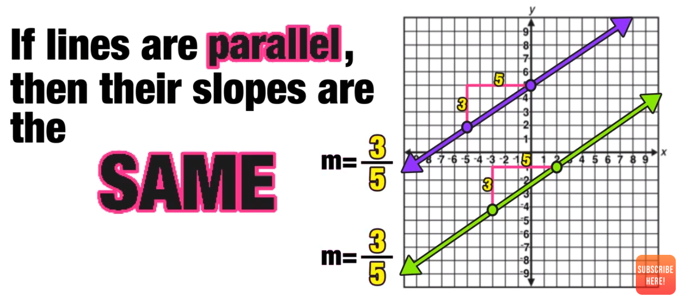
Parallel Lines
Never intersect
Have the SAME SLOPE (m)
For example, observe the purple line and the green line in Figure 1 below. These lines are parallel and have the same slope of m=3/5.
This is true for all parallel lines.
Figure 1
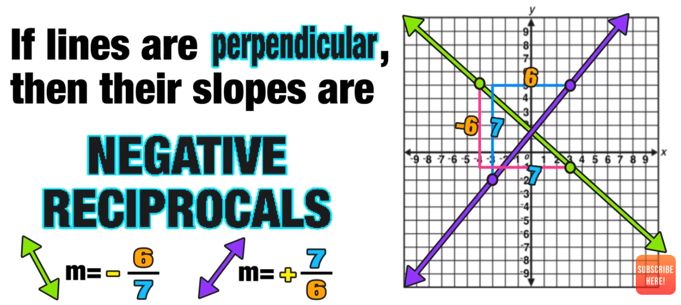
Perpendicular Lines
Intersect to Form Right Angles
Have the NEGATIVE RECIPROCAL SLOPES (m)
For example, observe the purple line and the green line in Figure 2 below. These lines are perpendicular and have negative reciprocal slopes.
Another way of saying negative reciprocal is FLIP AND SWITCH, which means to take the slope of the first line, flip the fraction and switch the sign (positive to negative or vice versa).
In this case, the green line slope is -(6/7) and the purple line slope is +(7/6)
This is true for all perpendicular lines.
Figure 2
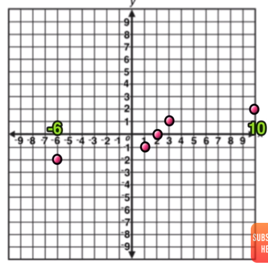
Parallel Slope Example
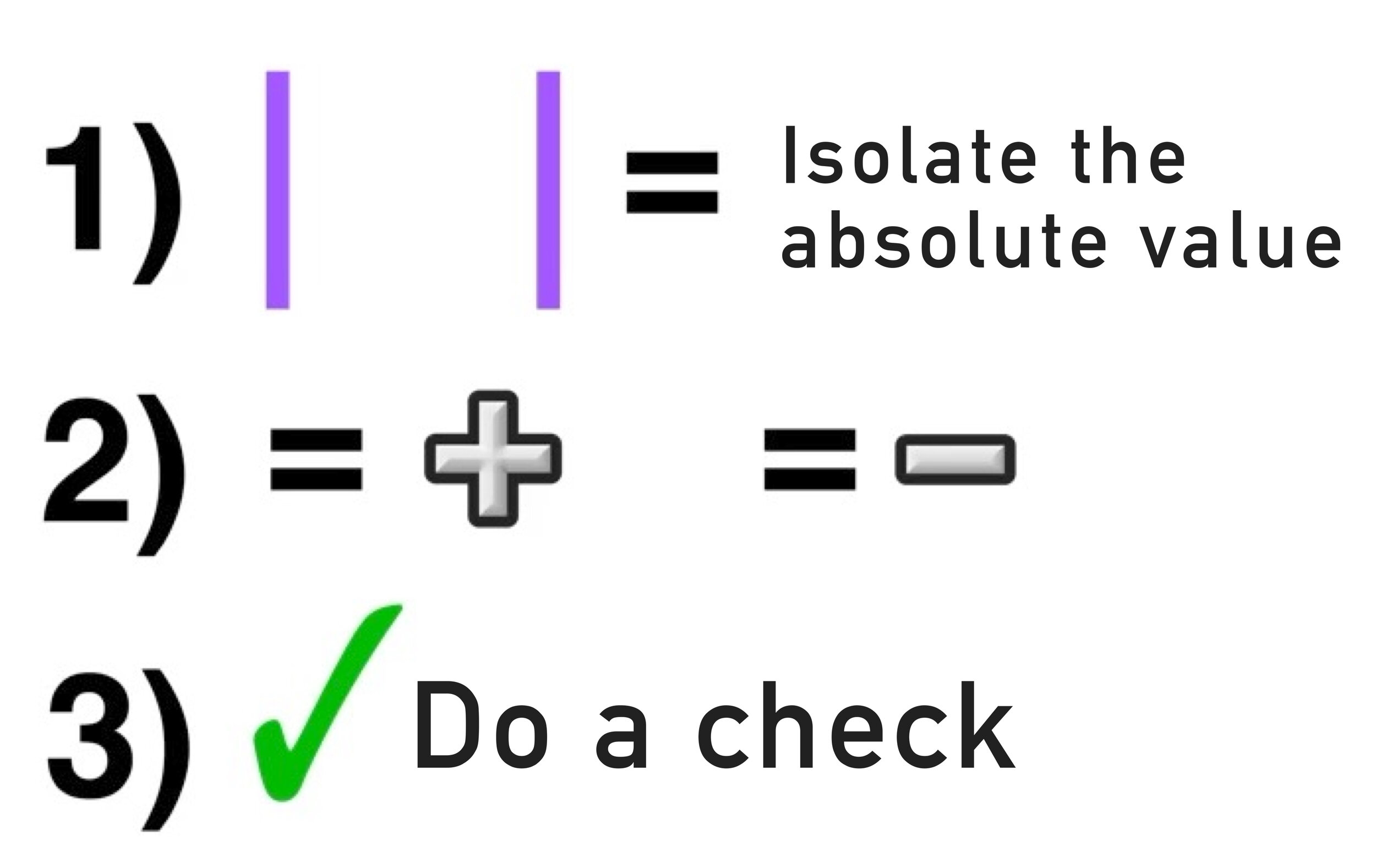
Example:
Let’s start by identifying the key information:
Since you have to graph a line through point J that is PARALLEL to line S, then you know that you will be dealing with SAME SLOPE.
Start by finding the slope of line S by finding the slope between the two given points (-4,0) and (5,2). You can find the slope by counting “rise over run” or by using the slope formula.
In this example, Line S has a slope of m=2/9.
Again, since parallel lines have the same slope, you can build your new line through point J by repeating the slope m=2/9 starting at point J as follows:
Now that you have plotted a new point using the same slope, the final step is to construct a line that passes through the new point and point J as follows:
And you have graphed your parallel line using slope!
Perpendicular Slope Example
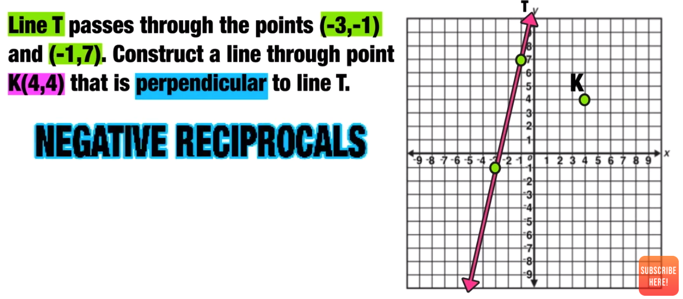
Example:
Figure 1
Start by identifying the key information.
Since you have to graph a line through point K that is PERPENDICULAR to line T, then you know that you will be dealing with NEGATIVE RECIPROCAL SLOPES (also known as “flip and switch”).
Start by finding the slope of line T by finding the slope between the two given points (-3,-1) and (-1,7). You can find the slope by counting “rise over run” or by using the slope formula.
In this example, Line T has a slope of m= +8/2, which simplifies to m=+4/1
Now that you know that the slope of Line T is m=+(4/1), you are ready to find the slope of the new line by finding the negative reciprocal.
You can do this taking the slope of Line T and doing “flip and switch”.
To do this, flip the fraction and switch the sign as follows:
The las step is to use the negative reciprocal to build your new line. You can do this by starting at point K and going down one unit and to the right four units (rise: -1, run: +4) and then plot a new point.
Now that you have plotted a new point using the negative reciprocal slope, the final step is to construct a line that passes through the new point and point K as follows:
And you have graphed your parallel line using slope!
Still Confused?
Check out this animated video tutorial on slopes of parallel and perpendicular lines and graphs:
Looking for more practice with graphing and slope?
Check out the following free resources:
Free Tutorial
Intro: Slope of a Line in Y=MX+B Form
Finding the Equation of a Line Using Two Points!
Keep Learning with More Free Lesson Guides:
Have thoughts? Share your thoughts in the comments section below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.