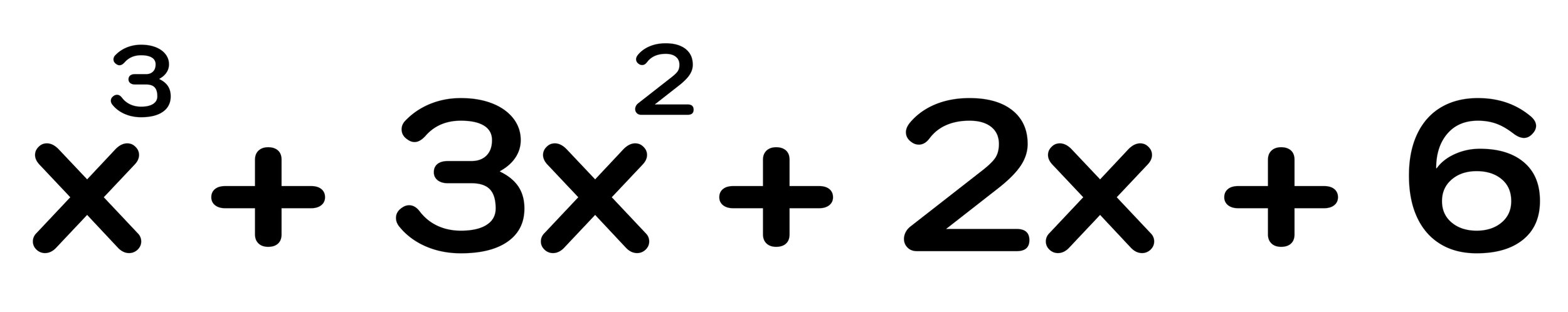What is the Easiest Math in College?

What is the Easiest Math in College?

What is the Easiest Math in College?

How to Choose College Math Courses That Work for You

 

What is the easiest math in college? While the answer depends on your skill level and career interests, there are several college math courses that are manageable and generally easy for students who want to avoid highly challenging courses like calculus.

(Image: Mashup Math via Getty)

 

Choosing college math classes that are appropriately challenging for you can be tricky. On one hand, you never want to put yourself in a math class that is extremely difficult where you are not in a position to be successful, which only wastes your time and money. On the other hand, it may not be valuable for you to take a college math class that is too easy or that focuses on material that you have mastered or is not useful to your potential career path.

It can be tricky to enroll in math classes that are a good fit for you, which is why so many students wonder what is the easiest math in college? If you find yourself asking this question as you begin to make your schedule, then continue reading for some solid advice and tips that will help you moving forward.

For starters, you are not alone. Many college students struggle with mathematics and want to enroll in courses that are manageable and not overly challenging. But determining the easiest math in college is not a simple determination, as the word “easiest" typically means something different for every student. However, in this post, we will explore some great options for students who are looking for a math class that is considered easy (i.e. less challenging) along with some helpful tips on how to pick math courses that will be a good fit for you.

Now, let's talk about what is meant by the easiest math in college. For some, easy math means courses that are appropriately challenging based on your individual skill level. These “Goldilocks” math classes are not too hard or too easy, instead, they are just right. For others, easy math means classes that require very little effort and often are not very challenging or interesting. Before moving forward, you will have to determine which definition of “easy math” applies to you.

Making this distinction is important because, just because a math class is considered easy, it doesn’t necessarily mean that the course will be a good fit for you and your potential career path. As a student, it is in your best interest to select math courses that are not only manageable, but also appropriately challenging, interesting, and engaging.

With this in mind, here are a few options for math classes that are generally considered to be easy and manageable for college students:

 

Statistics courses can be more manageable for some students because the material is less theoretical and more applied than more complicated math courses such as differential equations. Photo by Sam Balye on Unsplash

 

What is the Easiest Math Class in College?

  • Statistics: Statistics is a branch of mathematics dealing with the collection, analysis, and interpretation of numerical data. Statistics is often used in career fields including business, finance, research, and healthcare. Statistics courses can be more manageable for some students because the material is less theoretical and more applied than more complicated math courses such as differential equations.

  • Finite Math: Finite math refers to a variety of math courses that do not involve calculus. These types of course typically cover topics such as linear algebra and probability. This type of math is often used in business and the social sciences. Finite math classes are often a good option for students who want to avoid calculus.

  • Business Math: Business math courses focus on all of the practical applications of mathematics in business, such as finances, forecasting, and management. Business math topics often include percentages, interest, and applied algebra. Such courses can be a great option for students who are interested in business careers, but want to avoid abstract math courses that are overly challenging.

  • Applied Math: Also known as “Real-World Math,” applied math courses are designed to give students experience with math skills that are applicable to real life. These courses include topics such as logic, probability, and personal finance. Applied math courses are a good option for students who want to fulfill a math requirement, but are not interested in further pursuing any advanced math courses.

 

What is the easiest math class in college? The math classes you choose will be based on your personal goals and career aspirations. Photo by Desola Lanre-Ologun on Unsplash

 

What is the Easiest Math in College: Tips and Pointers

Now that you have a few good options for math courses that are generally considered to be easy, we can take a look a few pointers for college students on how to select math courses that will be a good fit for them:

  • Work with your advisor: Your academic advisor or guidance counselor can be a great resource for guiding you when choosing a math course that is appropriately challenging for your skill level and personal interests. Advisors can provide guidance on which math courses are requirements for your desired major and which courses could potentially be a good fit for you based on your interests.

  • Do your research: Before you enroll in any math class, it is important to do some research to find out what the course covers and what the course requirements are. This information can often be found in your school’s course catalog or website. This information will give you a better idea of whether or not a math class is a good fit for you and your interests.

  • Look for Reviews: Whenever possible, read course reviews online or talk to other students who have already taken the course. This type of feedback will give you insight into the what you will learn, the course’s difficulty level, and the teaching style of the professor.

  • Be Goal-Oriented: Choosing courses is often based on whatever major or minor you are pursuing, many of which include required math courses. Whenever you are choosing a math class to enroll in, think about why you are taking the course and what you hope to gain from being enrolled. You may simply be looking to fulfill a requirement, but you may also be interested in pursuing a career that requires strong math skills and you want to be more well-rounded.

  • Be Honest: Finally, always be honest with yourself and your skill level and comfort with mathematics. It’s okay to avoid math classes that may be too challenging for you or way too high above your skill level, but it’s never recommended to set your bar too low and choose math classes only because they are considered easy. Rather, if a math class that may be a requirement for a career path that interests you seems too challenging at the moment, talk to an advisor to find prerequisite courses that will help you develop your skills to a point where you are able to take on more challenging courses.

More Free Resources You Will Love:

Why Am I So Bad at Math? (And How to Get Better)

If you are wondering, why am I so bad at math? The fault is likely due to you having a fixed mindset for learning, which is often a product of being negatively affected by harmful misconceptions about your ability to learn math.

How to Engage Students in Math Lessons—5 Ideas

How to Engage Students in Math Lessons—5 Ideas

How to Engage Students in Math Lessons

5 Effective Ideas for How to Engage Students in Math Lessons

 

How to Engage Students in Math Lessons: Engagement in math starts with making the subject more interesting, relevant, and approachable for your students.

(Image: Mashup Math via Getty)

 

When students have negative attitudes about mathematics and its relevance to real life, they can quickly become disinterested in the subject, which often leads to disengagement and apathy in the classroom. As a teacher, you can flip the script on students’ mindset for math and its usefulness by utilizing strategies that allow them to experience math in a way that is both interesting and engaging. If you are looking for effective strategies for engaging your math students, below you will find five great ideas for making your upcoming lessons enjoyable and captivating for students at any grade level.

(Do you want free K-8 math resources, worksheets, and lesson plans in your inbox every week? Click here to receive our free newsletter in your inbox every week)

1.) Use Real-Life Examples

One of the most effective strategies you can use to engage students in math is to incorporate relatable real-life examples and applications. For example, when teaching fractions, you could use pizza slices to show how to divide a pizza into equal parts. Or when teaching geometry, you could use a map to show how streets and avenues resemble parallel lines and transversals. By using real-life examples, you can make math more tangible and relevant to your students' lives.

Suggested Link: 10 Examples of Real-World Connections in Math

 

How to Engage Students in Math Lessons: Use real-world examples to explore math concepts such as parallel lines and transversals.

 

2.) Use Technology

Technology can be a great tool to engage students in math. There are many educational apps and websites that can make learning math fun and interactive. For example, you could use online math games or interactive simulations to teach concepts such as algebra or geometry. You could also use digital tools such as graphing calculators or virtual manipulatives to help students visualize math concepts.

Suggested Link: Virtual Math Manipulatives—Free Library for Grades K-8

Suggested Link: Kid-Safe YouTube: A Safer Online Learning Experience for Students

 

How to Engage Students in Math Lessons: Use virtual math manipulatives to explore topics like fractions.

 

3.) Encourage Collaboration

Collaboration can be a powerful tool to engage students in math. By working together, students can share their ideas, learn from each other, and build confidence in their math skills. You could encourage collaboration by having students work in pairs or small groups on math problems or projects. You could also create a class math challenge or competition to encourage teamwork and friendly competition.

Suggested Link: How to Boost Student Engagement with Math Pictures

 

How to Engage Students in Math Lessons: Make math learning a team effort by encouraging collaboration. Photo by National Cancer Institute on Unsplash

 

4.) Provide Meaningful Feedback

Providing meaningful feedback can help students stay motivated and engaged in math. It also helps students to embrace a growth mindset for learning and not become easily discouraged by mistakes. When giving feedback, try to focus on specific strengths and areas for improvement. Another way to provide meaningful feedback is to give your students opportunities to reflect on how well they understand a given lesson or topic and to set personal learning goals for the future. When you provide your students with meaningful feedback, you are helping them to understand the benefits of their effort and individual progress and how it relates to the learning process.

Suggested Link: What is a Growth Mindset for Learning in Math?

 

How to Engage Students in Math Lessons: Meaningful feedback helps to keep students on track. Photo by Centre for Ageing Better on Unsplash

 

5.) Make Math Relevant

The final strategy for engaging your math students is to focus attention on how math is relevant to the real world and your students’ personal lives. When students understand how mathematics plays a role in nearly every aspect of life in some shape or form, they are much more likely to appreciate the subject and its usefulness. One way to make math relevant to your students is to incorporate real-world problems into your lessons. For example, you can combine math and finances when teaching a lesson on calculating percent increase or decrease. Another example is to share how being able to create and read data charts and graphs applies to a variety of fields including medical research, engineering, and technology.

Suggested Link: What is STEAM Education and Why is it Important?

 

How to Engage Students in Math Lessons: Math is all around us and it’s important for your students to understand its relevance to real life. Photo by ThisisEngineering on Unsplash

 

Not all math lessons are created equally. If you want to boost student participation, progress, and interest in learning, then you need to design lesson plans that are engaging and relevant to students. There are several strategies that you can use to make your math lessons more engaging for students, including:

  • Using Real-Life Examples

  • Incorporating Technology

  • Encouraging Collaboration

  • Providing Meaningful Feedback

  • Making Math Relevant

When your students are engaged and vested in learning math, they are more likely to stick with the subject as they move onto high grade levels and they will also have more career opportunities down the road.

More Free Resources You Will Love:

Where is the Bermuda Triangle?—Bermuda Triangle Map

Where is the Bermuda Triangle?—Bermuda Triangle Map

Bermuda Triangle Map—Where is the Bermuda Triangle?

Where is the Bermuda Triangle? New Detailed Bermuda Triangle Map Defines its Exact Location Using Google Maps

 

Where is the Bermuda Triangle located on Google Maps? (click to enlarge)

 

The Bermuda Triangle, also known as the Devil's Triangle, is a geographic region in the western part of the North Atlantic Ocean where many planes and ships have disappeared under mysterious circumstances.

Creating an accurate Bermuda Triangle map can be difficult because there are actually no fixed coordinates for the vertices of the Bermuda Triangle, since the region itself is not an officially recognized area, and its boundaries are not particularly well-defined.

Where is the Bermuda Triangle located on Google Maps? While the Bermuda Triangle is not an officially recognized area, it is possible to display the Bermuda Triangle on a map since its boundaries are generally considered to be between Miami, Bermuda, and Puerto Rico (each location being one of the three points of the triangle)

While the Bermuda Triangle map above (and the alternate version below) is generally considered the most accurate representation of a map of Bermuda Triangle, some sources actually consider the Triangle to extend as far north as Massachusetts and as far south as the Caribbean. However, these sources are in the minority, as the majority of accounts of ships or planes mysteriously going missing are within the boundaries of the Bermuda Triangle contained by Miami, Puerto Rico, and the island of Bermuda.

 

Bermuda Triangle Map: The boundaries of the Bermuda Triangle are generally considered to be between Miami, Bermuda, and Puerto Rico.

 

How Much Area is Occupied by the Bermuda Triangle on a Map?

Since the region that makes up the Bermuda Triangle is not well-defined, its geographic area can only be estimated. Generally speaking, it is said to cover an area of approximately 500,000 to 1.5 million square miles (or about 1.3 to 3.9 million square kilometers) of open ocean.

Despite the many claims of ships and planes mysteriously going missing within this triangular region, the scientific evidence supporting the idea that the Bermuda Triangle is supremely dangerous is lacking. In fact, most evidence suggests that the Triangle is really no more dangerous than any other part of the ocean. But the idea that the Bermuda Triangle is a relatively safe region for sea and air travel has not always been a popular belief, which is why the modern day map of the Bermuda Triangle is a product of several iterations made over the past several decades.

 

If there is no scientific evidence to suggest that the Triangle is dangerous compared to other areas of the ocean, then why have governments and militaries been so interested in accurately showing the Bermuda Triangle on a map?

 

Bermuda Triangle on a Map: History

If you were to search for the Bermuda Triangle on a map today, you would find that it is roughly bounded by Miami, Bermuda, and Puerto Rico. On a map, you can draw three lines connecting these three points to form the “Bermuda Triangle.” Within this triangular region is where the majority of incidents of missing ships and planes have been reported. However, the region known as the Bermuda Triangle is actually not officially recognized by any science, government, or military organization, and there is zero evidence to supporting the idea that the region is supernaturally dangerous.

Still, the Bermuda Triangle continues to be an area of interest and many maps of the region have been created over the years, each containing its own unique features. For example, some maps of the Bermuda Triangle plot the locations of any reported disappearances of ships or planes. Other maps try to highlight potential explanations for the phenomenon, such as atmospheric anomalies and unusual weather patterns.

One of the most famous maps of the Bermuda Triangle was created by Charles Berlitz in his 1974 book The Bermuda Triangle. Like the modern map, Berlitz’ version also has the vertices of the Bermuda Triangle at Puerto Rico, Bermuda, and Miami, Florida. His version includes red dots scatted around the region—each one representing a reported disappearance of a ship or airplane. However, from a modern lens, Berlitz’s map is not entirely accurate and it may include disappearances that are not actually verified or ones that did occur, but not inside of the Bermuda Triangle.

 

The 1974 book The Bermuda Triangle by Charles Berlitz. Image used as fair use to
illustrate article subject.

 

The U.S. Navy also created a Bermuda Triangle map in 1968. The Navy's depiction of the Bermuda Triangle is a region that is much smaller than typical maps, but with similar boundaries (the Navy also has the vertices of the Triangle being at Bermuda, Puerto Rico, and the southern tip of Florida). Interestingly, the Navy's Bermuda Triangle map includes a note saying that "the area is one of the most heavily traveled shipping lanes in the world, and commercial and pleasure craft routinely navigate through it without incident." This military version of the map stresses that the Bermuda Triangle is not an official region and or an area that is particularly dangerous.

There are also maps of the Bermuda Triangle that present potential explanations for the reported disappearances. One theory is that methane gas hydrates located beneath the ocean floor could be causing ships to sink by reducing the buoyancy of the water. Another theory suggests that unusual weather patterns or ocean currents in the area could be responsible for the incidents.

 

The US Navy began mapping the Bermuda Triangle in 1968. Photo by Abdullah Al Hasan on Unsplash

 

Whether the explanation as to why so many ships and planes have gone missing in the region known as the Bermuda Triangle is scientific or supernatural, the jury is still out. Either way, the region itself will always be a point of interest and fascination for many, which is why establishing the boundaries of the region on a Bermuda Triangle map is so important.

More Free Resources You Will Love:

Search Tags: where is the bermuda triangle, bermuda triangle map, bermuda triangle on a map, map of bermuda triangle, bermuda triangle on map, map bermuda triangle, map of the bermuda triangle, where is the bermuda triangle located on google maps, bermuda triangle location on map

How to Factorize a Cubic Polynomial

2 Comments

How to Factorize a Cubic Polynomial

How to Factorize a Cubic Polynomial

Step-by-Step Guide: How to Factor a Cubic Polynomial in 3 Easy Steps

 

Free Step-by-Step Guide: How to factor a polynomial with a specific number of terms

 

In algebra, a cubic polynomial is an expression made up of four terms that is of the form:

  • ax³ + bx² + cx + d

Where a, b, c, and d are constants, and x is a variable. Polynomials in this form are called cubic because the highest power of x in the function is 3 (or x cubed).

Unlike factoring trinomials, learning how to factorize a cubic polynomial can be particularly tricky because using any type of guess-and-check method is extremely difficult. However, you can easily learn how to factor a cubic polynomial by using the grouping method described in this guide.

This free Step-by-Step Guide on How to Factorize a Cubic Polynomial will cover the following key topics:

While learning how to factor cubic polynomials can be challenging at first, you can develop your skills pretty quickly just by working through practice problems step-by-step until you become more comfortable with factoring cubic polynomials. So, this guide was designed to teach you everything you need to know about how to factor a cubic polynomial. We recommend that you read through this guide from start to finish and work through each example by following along step-by-step. By the end, you will be able to quickly and accurately factorize a cubic polynomial.

 

Figure 01: How to Factorize a Cubic Polynomial

 

What is a cubic polynomial?

As previously mentioned, a cubic polynomial is a math expression that is of the form ax³ + bx² + cx + d, where a, b, c, and d are all constants and x is a variable, and typically has four terms. Note that x is not the only letter that can be used as a variable in a cubic polynomial. Also, the number in front of any variable is referred to as a coefficient.

Additionally, the terms of a cubic polynomial are the individual “pieces” of the expression, separated by an addition or subtraction sign.

For example, the cubic polynomial in Figure 01 above, x³ + 3x² + 2x + 6 has four terms:

  • 1st Term: x³

  • 2nd Term: 3x²

  • 3rd Term: 2x

  • 4th term: 6

Before you can learn how to factor a cubic polynomial, it is extremely important that you know how to recognize that given polynomial is cubic, so make sure that you deeply understand what a cubic polynomial is before moving forward in this guide.

 

Figure 02: Factoring a Cubic Polynomial

 

What does it mean to factorize a cubic polynomial?

In math, the factors of any polynomial represent components or “building blocks” of the polynomial. Whenever you factor a polynomial (cubic or otherwise), you are finding simpler polynomials whose product equals the original polynomial. Each of these simpler polynomials is considered a factor of the original polynomial.

For example, the binomial x² - 100 has two factors (x + 10) and (x-10).

Why? Lets take a look at what happens when we find the product of the factors by double distributing:

  • (x+10)(x-10) = x² + 10x - 10x - 100 = x² + 0 - 100 = x² - 100

Notice that the result was the original polynomial, x² - 100.

Since cubic polynomials (four terms) are more complex than binomials (two terms), their factors will also be a little more complex, but the idea is still the same—factoring a cubic polynomial involves finding simpler polynomials or “building blocks” whose product is the original cubic polynomial.

And, to factorize a cubic polynomial, we will be using a strategy called grouping that will allow you to factor any cubic polynomial (assuming that it is factorable at all) using 3 easy steps. So, lets go ahead and work three practice problems to give you some experience with factoring cubic polynomials by grouping.

Now that you understand the key terms and the difference between a polynomial with 2 terms, 3 terms, and 4 terms.

For factoring each type of polynomial, we will look at two methods: GCF, direct factoring, and, sometimes, a combination of the two.

Let’s get started!

How to a Factorize a Cubic Polynomial Examples

Now, you will learn how to use the follow three steps to factor a cubic polynomial by grouping:

Step One: Split the cubic polynomial into two groups of binomials.

Step Two: Factor each binomial by pulling out a GCF

Step Three: Identify the factors

As long as you follow these three steps, you can easily factor a given polynomial, though note that not all cubic polynomials are factorable."

We will start by factoring the cubic polynomial shown in Figure 01: x³ + 3x² + 2x + 6

Example #1: Factor x³ + 3x² + 2x + 6

 

Figure 03: We have to find the factors of x³ + 3x² + 2x + 6

 

To factorize this cubic polynomial, we will be applying the previously mentioned 3-step method as follows:

Step One: Split the cubic polynomial into groups of two binomials.

To factor this cubic polynomial, we will be using the grouping method, where the first step is to split the cubic polynomial in half into two groups.

 

Figure 04: The first step to factoring a cubic polynomial is to split it into groups of two binomials.

 

For Example #1, at the end of the first step, you have split the cubic binomial down the middle to form two groups of binomials:

  • (x³ + 3x²)

  • (2x + 6)

Why are you splitting the cubic polynomial like this? Notice that it is not possible to pull a Greatest Common Factor (GCF) out of the original cubic polynomial x³ + 3x² + 2x + 6. The goal of the first step is to create two separate binomials, each with a GCF that can be “pulled out.”

 

Figure 05: Make sure that each individual binomial has a GCF before moving onto the next step.

 

Step Two: Factor each binomial by pulling out a GCF

Again, the purpose of the first step is to split the cubic polynomial into two binomials, each with a GCF. Before moving forward, ensure that each individual binomial has a GCF; otherwise, you may need to swap the positions of the middle terms (3x² and 2x). Swapping these middle terms is not required for this first example; however, we will work through an example later on where this is required.

Now, for step two, you can divide the GCF out of each grouping as follows:

  • (x³ + 3x²)→ x²(x +3)

  • (2x + 6) → 2(x + 3)

This process of pulling the GCF out of each binomial is illustrated in Figure 05 below.

 

Figure 06: To factorize a cubic function, split it into two groups and then pull a GCF out of each group.

 

Step Three: Identify the factors

After completing the second step, you are left with:

  • x²(x +3) + 2(x+3)

Notice that both groups share a common term, which, in this case, is (x+3). This result is expected and is a signal that you are factoring the cubic polynomial correctly. If the groups do not share a common terms, then it is likely that the cubic polynomial is not factorable or that you made a mistake pulling out the GCF.

However, since you factored each group and ended up with a common factor of (x+3), you can move on to determining the factors of the cubic polynomial.

The illustration in Figure 06 above color-codes how you use the results from step two to determine the factors of the cubic polynomial.

You already know that one of the factors is (x+3). To find the other factor, you can simply take the two “outside” terms, in this case, x² and +2.

  • x²(x +3) + 2(x+3) → (x²+2)(x+3)

Final Answer: The factors of x³ + 3x² + 2x + 6 are (x²+2) and (x+3)

The entire 3-step method that we just used to factor a cubic polynomial by grouping is shown in Figure 07 below:

 

Figure 07: How to factorize a cubic polynomials step-by-step

 

How can you check if your factors are actually correct? You can perform double distribution to multiply the binomials together to see if the result is indeed the cubic polynomial that you started with. If it is, then you know that you have factorized correctly.

You can see in Figure 08 below that multiplying the factors together does indeed result in the original cubic polynomial, so you know that your factors are correct:

  • (x²+2)(x+3) = x³ + 3x² + 2x + 6

 

Figure 08: Check your answer using double distribution

 

Now, lets go ahead and work through another example of how to factor a cubic polynomial.

Example #2: Factor 2x³ - 3x² + 18x - 27

Just like in the first example problem, you can use the 3-steps for factoring a cubic polynomial by grouping as follows:

 

Figure 09: Find the factors of the cubic polynomial 2x³ - 3x² + 18x - 27

 


Step One: Split the cubic polynomial into groups of two binomials.

After splitting this cubic polynomial, you end up with these two groups: (2x³ - 3x²) and (18x-27)

 

Figure 10: Step One: Split the cubic polynomial into two groups

 

Step Two: Factor each binomial by pulling out a GCF

Next, divide a GCF out of each group (if possible) as follows:

  • (2x³ - 3x²) → x²(2x - 3)

  • (18x - 27) → 9(2x - 3)

This process of pulling a GCF out of each group is illustrated in Figure 11 below:

 

Figure 11: Factorize a cubic polynomial

 

Step Three: Identify the factors

Since both factors have a common term, (2x-3), you know that you have likely factored correctly and you can move onto identifying the factors.

Final Answer: (x²+9) and (2x-3) are the factors of the cubic polynomial 2x³ - 3x² + 18x - 27.

All of the steps for solving Example #2 are illustrated in Figure 12 below.

 

Figure 12: The factors are (x²+9) and (2x-3)

 

Just like the last example, you can check to see if your final answer is correct by multiplying the factors together and seeing if the result equals the original cubic polynomial.

Example #3: Factor 3y³ + 18y² + y + 6

Finally, lets work through one more example where you have to factorize a cubic polynomial.

Step One: Split the cubic polynomial into groups of two binomials.

Again, the first step is to split the cubic polynomial down the middle into two binomials as shown in Figure 13 below.

 

Figure 13: Factoring a cubic polynomial by grouping.

 

As shown in Figure 13 above, splitting the polynomial down the middle leaves you with these two groups: (3y³ +18y²) and (y+6)

Remember that the whole point of splitting the cubic polynomial is to create two binomials that each have a GCF. But notice that the second binomial, (y+6), is not factorable because there is no GCF between +y and +6.

But, as previously mentioned, this doesn’t mean that you can not solve this problem further. In fact, the commutative property of addition allows you to swap the positions of the two middle terms (18y² and +y).

This extra step of swapping the two middle terms is illustrated in Figure 14 below.

 

Figure 14: Sometimes you have to swap the positions of the middle terms in order to factorize a cubic polynomial.

 

After swapping the positions of the middle terms, you can now apply the 3-step method to factoring the equivalent polynomial: 3y³ + y + 18y² + 6 (this new cubic polynomial is equivalent to the original because the commutative property of addition allows you to rearrange the terms without changing the value of the expression).

Now, you actually can split the new cubic polynomial into groups that can be factoring by dividing out a GCF: (3y³ + y) and (18y² + 6)

 

Figure 15: After swapping the positions of the middle terms, you can continue on with factoring the cubic polynomial.

 

Step Two: Factor each binomial by pulling out a GCF

As shown in Figure 15 above, you can factor each group by pulling out a GCF as follows:

  • (3y³ + y) → y(3y² + 1)

  • (18y² + 6) → 6(3y² + 1)

Step Three: Identify the factors

Finally, you can conclude that:

Final Answer: The factors are (y+6) and (3y² + 1)

The step-by-step process to solving this 3rd example are shown in Figure 16 below. Again, you can make sure that your final answer is correct by multiplying the factors together and verifying that their product is equivalent to the original cubic polynomial.

 

Figure 16: How to factorize a cubic polynomial when you have to swap the middle terms.

 

How to Factorize a Cubic Polynomial: Conclusion

It is beneficial to understand how to factorize a cubic polynomial because the skill will allow you to simplify and understand the behavior of cubic functions as you continue onto higher levels of algebra and begin to explore topics like finding roots, analyzing graphs, and solving cubic equations.

Factoring cubic functions can be challenging, but you can always use the following 3-step grouping method described in this guide to successfully factor a cubic polynomial (assuming that it is factorable in the first place):

Step One: Split the cubic polynomial into groups of two binomials.

Step Two: Factor each binomial by pulling out a GCF

Step Three: Identify the factors

Keep Learning:

2 Comments

March Madness Perfect Bracket Odds—What are the Chances?

1 Comment

March Madness Perfect Bracket Odds—What are the Chances?

What are the March Madness Perfect Bracket Odds?

The Chances of a Perfect March Madness Bracket are Crazier Than You Might Think

 

Is this possible? What are the March Madness perfect bracket odds?

 

The annual NCAA College Basketball Tournament—known as March Madness—is one of the most exciting times of the year for college basketball fans. Every year, millions of fans across the United States fill out their tournament brackets, hoping to predict the winners of all 63 games. But what are the chances of filling out a perfect March Madness bracket? Is it even possible?

Let’s explore the math behind why a predicting a perfect March Madness bracket is essentially impossible by diving into the answers to the following questions:

 

Every year, millions of fans fill out a tournament bracket. What what are the chances of a perfect March Madness bracket?

 

What are the March Madness Perfect Bracket Odds?

Filling out a perfect March Madness bracket means correctly predicting the winner of all 63 NCAA basketball tournament games. Having a perfect bracket means that must be 100% correct in all of your picks, including all of the inevitable upsets (when a lower ranked team defeats a higher ranked team) that occur every year.

The mathematical probability of a perfect March Madness bracket are:

1 : 9,200,000,000,000,000,00.

You read that correctly. The chances of correctly predicting a perfect March Madness bracket are astronomically low. In fact, some mathematical models estimate the odds of having a perfect March Madness bracket at one in 9.2 quintillion.

To put it another way, you are more likely to win the lottery multiple times in a row or get struck by lightening twice on the same day than to fill out a perfect bracket.

 

Given the low odds of a perfect March Madness bracket, is it even possible? Photo by Hannah Gibbs on Unsplash

 

Is a March Madness perfect bracket even possible?

The short answer is no, it is not possible to fill out a perfect March Madness bracket given the insanely high odds of correctly predicting the winner of all 63 games.

The reason for saying that a March Madness perfect bracket is impossible is simple—there are just too many variables at play in every game that make predicting winners incredibly difficult.

Even the most talented and experienced basketball analysts and sports statistics experts can not predict with complete accuracy how a given tournament game will play out. Factors such as injuries to key players, momentum swings, and elements of chance can all play a role in the outcome of a basketball game. And when you consider that there are 63 games in the tournament, the chances of getting correctly predicting the winner of every single game is virtually zero.

Of course, the fact that a perfect March Madness bracket is essentially impossible should not discourage you from filling out a bracket and attempting to correctly predict the outcome of as many games as possible. Why? Because filling out a bracket and chasing this impossible dream is what makes March Madness such a fun time of year for die-hard and casual basketball fans alike.

Even if you don't have a perfect bracket, you can still compete with your friends and colleagues to see who can get the most games right. And who knows? You might just run into some luck and make some accurate predictions that others did not.

 

Has there ever been a perfect March Madness bracket? Photo by Jacob Rice on Unsplash

 

Has There Ever Been a Perfect March Madness Bracket?

Millions of basketball fans have been filling out March Madness brackets since the tournament’s inception in 1939, but has anyone ever had a perfect March Madness bracket?

The answer is no.

Remember that the odds of predicting the winners of all 63 tournament games are astronomically low, with some estimates placing the odds of a perfect bracket at around 1 in 9.2 quintillion.

Even with the rise of advanced analytics and machine learning algorithms, no one person has ever been able to achieve a perfect March Madness bracket, and they likely never will.

How Can You Use Math to Improve Your Bracket Predictions?

Mathematically speaking, filling out a perfect bracket is virtually impossible. But, what are your chances of getting a certain number of games right?

Let’s take a look at some statistics that will shed some light on this question.

According to the NCAA, the chances of correctly predicting the outcome of the first round (the 32 games played during the first two days of the tournament) are about 1 in 4.3 billion. While those odds are not very much in your favor, they are still way better than the odds of predicting a perfect March Madness bracket. In fact, there have been several occasions where someone correctly predicted the winners of all 32 first-round games.

 

The chances of predicting the winner of any NCAA tournament game depend on many factors including matchups, injuries, and past performance. Photo by Markus Spiske on Unsplash

 

But, as the tournament continues on into the later rounds, the odds of correctly predicting every winner become exponentially smaller. By the time you get to the third round (known as the Sweet 16), the chances of predicting all the games correctly are about 1 in 75.6 million.

As for the point in the tournament when only four teams remain (known as the Final Four), the odds of predicting all games correctly drop to about 1 in 2.4 million.

These odds are only estimates, and the actual chances of getting each game right can vary depending on many factors. The point is that, while the chances of a perfect March Madness bracket are essentially zero, it is still possible to correctly predict winners and have fun competing with others.

In fact, if you were to simply guess the winner of every March Madness game at random, without any knowledge or analysis of college basketball, you would be mathematically expected to correctly predict around half of the total games (about 31.5 out of the 63 games).

So, what should you keep in mind when filling out your March Madness bracket? The best advice we can give is to focus more on making educated based on information such as a teams’ record, matchups, current injuries, and recent performance. You can also take advice from trusted sports analysts and experts that can offer valuable insights that will help you make decisions when filling out your bracket.

 

Given that the March Madness perfect bracket odds are pretty much impossible, you can let yourself off the hook and simply have fun filling out your bracket. Photo by Ben Hershey on Unsplash

 

Another thing to keep in mind about filling out your bracket is the occurrence of upsets—when a lower ranked team wins against a higher ranked team. Upsets are incredibly common in the NCAA tournament and they are one of the most fun and exciting aspects of March Madness.

With this in mind, don't be afraid to pick a few lower-seeded teams to defeat a higher-seeded opponent, especially during the first two rounds.

On a final note, given that the March Madness perfect bracket odds are impossible, you can let yourself off the hook and simply have fun filling out your bracket, knowing that it will likely get busted during the first round.

The unpredictability of the tournament is what contributes to the 'Madness'—so have fun and good luck!

More Free Resources You Will Love:

Search Tags: march madness perfect bracket odds, chances of a perfect march madness bracket, perfect march madness bracket, odds of having a perfect march madness bracket, march madness perfect bracket, perfect march madness bracket odds, has there been a perfect march madness bracket, has anyone ever had a perfect march madness bracket, odds of a perfect march madness bracket, perfect bracket march madness

1 Comment