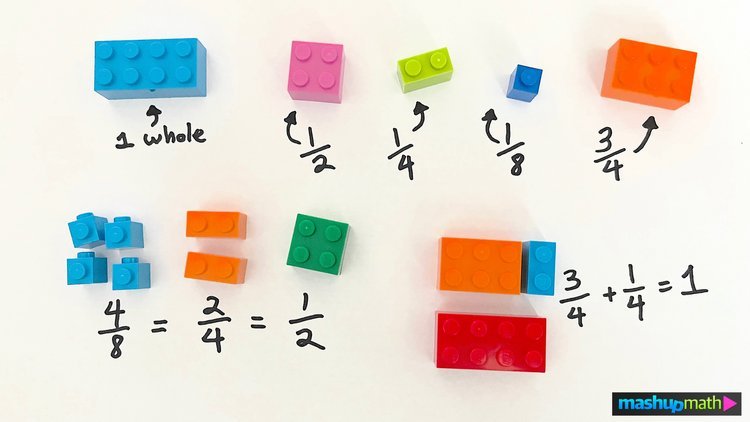How to Add Fractions in 3 Easy Steps

How to Add Fractions in 3 Easy Steps

Math Skills: How to add fractions with the same denominator and how to add fractions with different denominators

Knowing how to add fractions is an important and fundamental math skill.

Since fractions are a critically important math topic, understanding how to add fractions is a fundamental building block for mastering more complex math concepts that you will encounter in the future.

(Looking to learn how to subtract fractions? Click here to access our free guide)

Luckily, learning how to add fractions with like and unlike (different) denominators is a relatively simple process. The free How to Add Fractions Step-by-Step Guide will teach you how to add fractions when the denominators are the same and how to add fractions with different denominators using a simple and easy 3-step process.

This guide will teach you the following skills (examples included):

• What is the difference between the numerator and denominator of a fraction?

• How to add fractions with the same denominator?

• How to add fractions with different denominators?

But, before you learn how to add fractions, let’s do a quick review of some key characteristics and vocabulary terms related to fractions before we move onto a few step-by-step examples of how to add fractions.

Are you ready to get started?

How to Add Fractions: Definitions and Vocabulary

In order to learn how to add fractions, it is imperative that you understand the difference between a numerator and a denominator.

Definition: The numerator of a fraction is the top number in the fraction. For example, in the fraction 3/4, the numerator is 3.

Definition: The denominator of a fraction is the bottom number in the fraction. For example, in the fraction 3/4, the denominator is 4.

Pretty simple, right? These terms are visually represented in Figure 01 below. Make sure that you understand the difference between the numerator and the denominator of a fraction before moving forward in this guide. If you mix them up, you will not learn how to add fractions correctly.

Figure 01: The numerator is the top number of a fraction, and the denominator is the bottom number of a fraction.

Now that you know the difference between the numerator and the denominator of a fraction, you are ready to learn how to identify whether or not a given problem involving adding fractions falls into which of the following categories:

• Like Denominators (the denominators are the same)

• Unlike Denominators (the denominators are different)

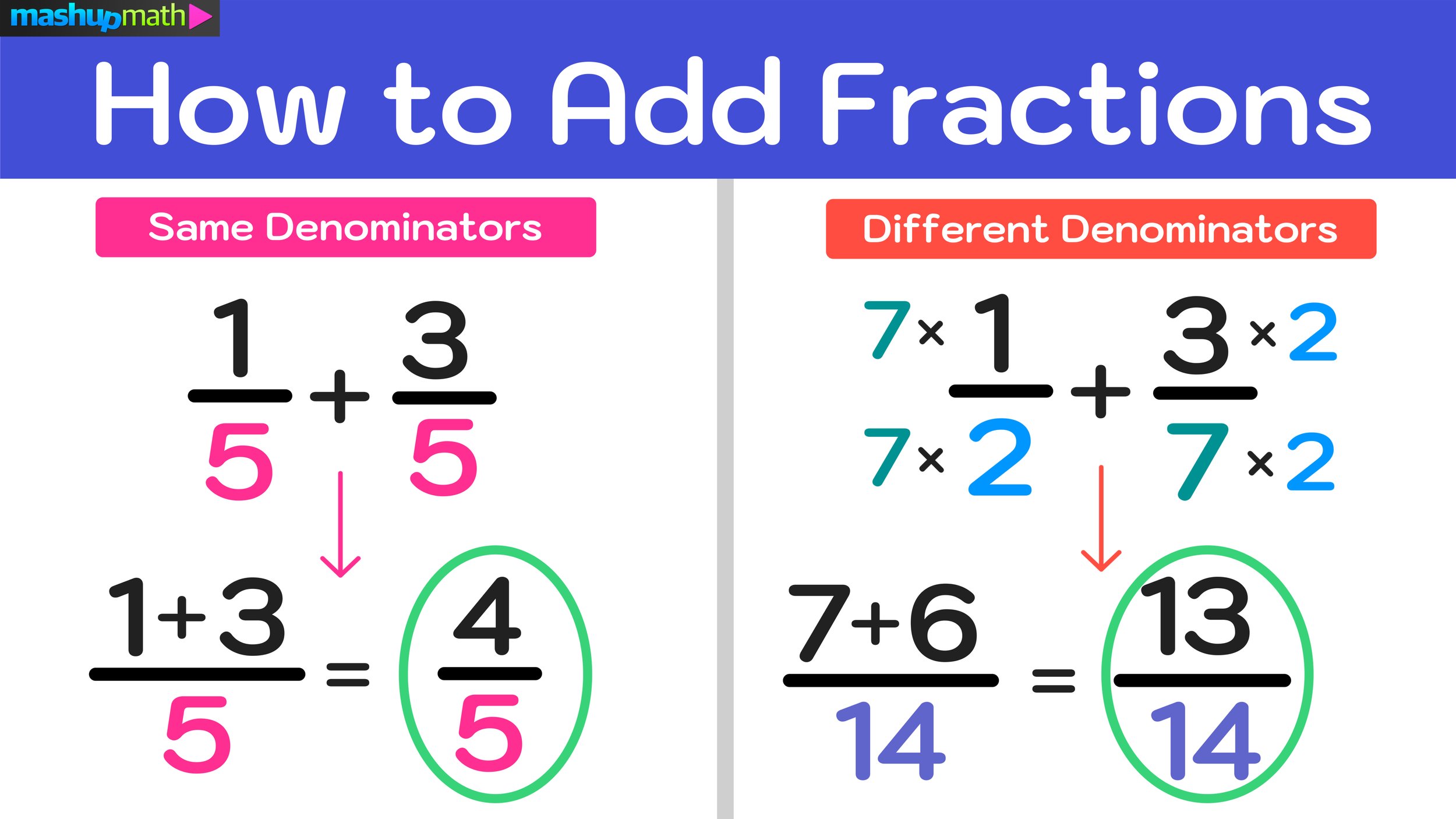
Fractions with like denominators have bottom numbers that equal the same value. For example, in the case of 1/5 + 3/5, you would be adding fractions with like denominators since both fractions have a bottom number of 5.

Conversely, fractions with different (or unlike) denominators have bottom numbers that do not equal the same value. For example, in the case of 1/2 + 3/7, you would be adding fractions with different denominators since the fractions do not share a common denominator (one has a denominator of 2 and the other has a denominator of 7).

These examples are featured in Figure 02 below.

Figure 02: In order to learn how to add fractions, you must be able to identify when the fractions have denominators that are the same and when they have different denominators.

Again, this concept should be simple, but a quick review was required because you will need to be able to identify whether or not a fractions addition problem involves like or unlike denominators in order to solve it correctly.

Now, let’s move onto a few examples.

---

How to Add Fractions with Like Denominators

How to Add Fractions with Like Denominators: Example #1

Example #1: 1/4 + 2/4

Our first example is rather simple, but it is perfect for learning how to use our easy 3-step process, which you can use to solve any problem that involves adding fractions:

• Step One: Identify whether the denominators are the same or different.

• Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

• Step Three: Add the numerators and find the sum.

Okay, let’s take our first attempt at using these steps to solve the first example: 1/4 + 2/4 = ?

Step One: Identify whether the denominators are the same or different.

Clearly, the denominators are the same since they both equal 4.

Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

Since the denominators are the same, you can move onto Step Three.

Step Three: Add the numerators and find the sum.

To complete this first example, simply add the numerators together and express the result as one single fraction with the same denominator as follows:

• 1/4 + 2/4 = (1+2)/4 = 3/4

Since 3/4 can not be simplified further, you can conclude that…

Final Answer: 3/4

This process is summarized in Figure 03 below.

Figure 03: How to Add Fractions: The process is relatively simple when the denominators are the same.

As you can see from this first example, learning how to add fractions when the denominators are the same is very simple.

To add fractions with the same denominator, simply add the numerators and keep the same denominator.

Let’s take a look at one more example of adding fractions when the denominators are the same before you learn how to add fractions with different denominators.

---

How to Add Fractions with Like Denominators: Example #2

Example #2: 2/9 + 4/9

To solve this second example, let’s apply the 3-step process like we did in the previous example as follows:

Step One: Identify whether the denominators are the same or different.

The denominators in this example are the same since they both equal 9.

Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

Again, you can skip the second step because the denominators are the same.

Step Three: Add the numerators and find the sum.

The final step is to add the numerators and keep the denominator the same:

• 2/9 + 4/9 = (2+4)/9 = 6/9

In this case, 6/9 is the correct answer, but this fraction can actually be reduced. Since both 6 and 9 are divisible by 3, 6/9 can be reduced to 2/3.

Final Answer: 2/3

This process is summarized in Figure 04 below.

Figure 04: How to Add Fractions: 6/9 can be reduced to 2/3

Next, let’s learn how to add fractions with different denominators.

---

How to Add Fractions with Different Denominators

How to Add Fractions with Different Denominators: Example #1

Example #1: 1/3 + 1/4

Step One: Identify whether the denominators are the same or different.

In this case, the denominators are different (one is 3 and the other is 4)

Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

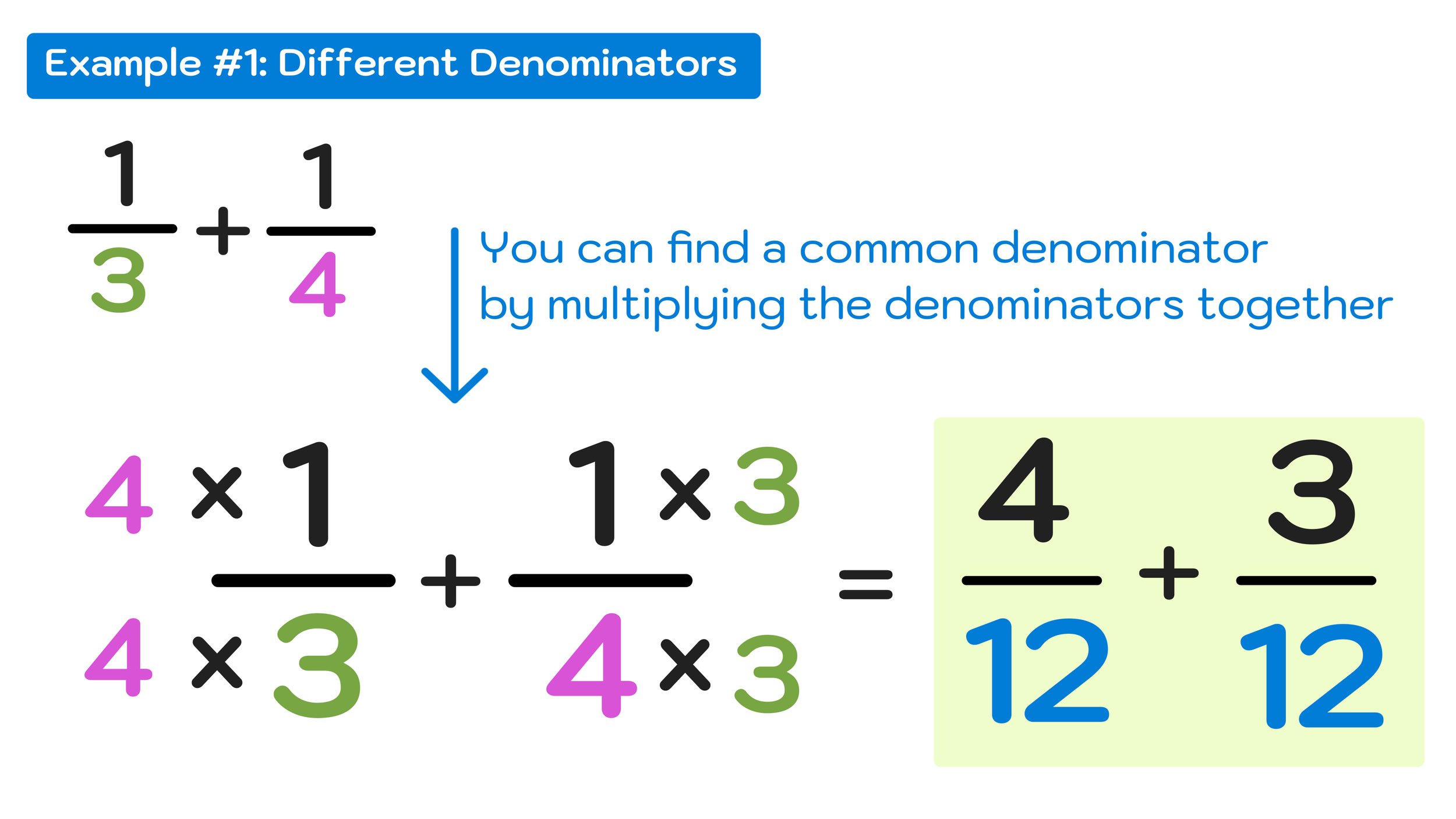
For this example, you can not skip the second step. Before you can continue on, you will need to find a common denominator—a number that both denominators can divide into evenly.

The easier way to do this is to multiply the denominator of the first fraction by the second fraction and the denominator of the second fraction by the first fraction (i.e. multiply the denominators together).

• 1/3 + 1/4 (4x1)/(4x3) + (3x1)/(3x4) = 4/12 + 3/12

This process is shown in Figure 05 below.

Figure 05: How to Add Fractions with Different Denominators: Get a common denominator by multiplying the denominators together.

(If you need some help with multiplying fractions, click here to access our free guide).

Now, we have transformed the original question into a scenario involving adding two fractions that do have common denominators, which means that the hard work is over and we can solve by adding the numerators and keep the same denominator:

• 4/12 + 3/12 = (4+3)/12 = 7/12

Since 7/12 can not be simplified further, you can conclude that…

Final Answer: 7/12

Figure 06: Once you have common denominators, you can simply add the numerators together and keep the same denominator.

Now, let’s work through one final example of adding fractions with unlike denominators.

---

How to Add Fractions with Different Denominators: Example #2

Example #1: 3/5 + 4/11

For this last example, let’s again apply the 3-step process:

Step One: Identify whether the denominators are the same or different.

The denominators are clearly different (one is 5 and the other is 11)

Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

Just like the last example, the second step is to find a common denominator by multiplying the denominators together as follows:

• 3/5 + 4/11 (11x3)/(11x5) + (5x4)/(5x11) = 33/55 + 20/55 = 53/55

This process is shown in Figure 07 below.

Figure 07: How to Add Fractions with Different Denominators: Get a common denominator by multiplying the denominators together.

Finally, now that you have common denominators, you can solve the problem as follows:

• 33/55 + 20/55 = (33+20)/55 = 53/55

Since there is no value that divides evenly into both 53 and 55, you can not simplify the fraction further.

Final Answer: 53/55

Figure 08: How to Add Fractions with Different Denominators: 53/55 can not be simplified further.

Conclusion: How to Add Fractions

To add fractions with the same denominator, simply add the numerators (top values) and keep the same denominator (bottom value).

To add fractions with different denominators, you need to find a common denominator. A common denominator is a number that both denominators can divide into evenly.

You can solve problems involving adding fractions for either scenario by applying the following 3-step process:

• Step One: Identify whether the denominators are the same or different.

• Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

• Step Three: Add the numerators and find the sum.

Keep Learning:

How to Subtract Fractions in 3 Easy Steps

---

Search Tags: how to add fractions, how to add fractions with different denominators, how to add fraction , how to add fractions with unlike denominators, how to. add fractions, how to add fractions with, how to add a fraction

Who Invented Math?—Explanation for Students

Who Invented Math?

A Quick Explanation of the History of Math for Students

Who invented math? Not Pythagoras, but his contributions to the field of mathematics are alive and well today.

The history of math runs deep and spans across a variety of ancient cultures and civilizations, which leads many to wonder who invented math?

Some people might think that mathematics just magically appeared out of thin air as if it were discovered in a dream, and many do believe that mathematics was somehow discovered rather than invented.

Either way, mathematics has not always been as broad and well understood as it is today. In fact, the field of mathematics has been evolving and growing over thousands of years, with contributions from various cultures and individuals.

Let's start our exploration of the question “who invented math?” with the ancient Babylonians, who developed a number system based on 60. This system is still used today in time and angle measurements, which is an absolutely extraordinary fact considering that the Babylonian number system dates back to approximately 1800 B.C. They were also skilled at solving quadratic equations, and they even had a form of algebraic notation. Since you can’t do math without numbers, the Babylonians deserve a lot of credit for laying the groundwork for modern day mathematics.

Who invented math? The ancient Babylonians developed one of the first number systems, but do they deserve all of the credit?

But who invented math? The Babylonians developed one of the first instances of numbers, but do they get the full credit?

Our next stop along the timeline of the history of math takes us to ancient Egypt. The ancient Egyptians had a great need for mathematics in order to build their pyramids and engineer their complex society, and they developed a system of mathematics that relied heavily on geometry. They were extremely talented at calculating areas and volumes, and they even had a formula for finding the volume of a truncated pyramid.

Who invented math? The ancient Egyptians made tremendous contributions to all fields of mathematics including geometry.

The ancient Egyptians made some unbelievable contributions to the field of mathematics, but it would be hard to say that they should get all of the credit for inventing math. But who could top the Egyptians?

Enter the ancient Greeks. These folks were absolute legends when it came to contributions in the field of mathematics. Of course, there was Plato, whose study of mathematics led him to classify the Platonic Solids as the building blocks of the universe. But the ancient Greeks also produced some of the greatest mathematical minds of all time, including Pythagoras, Euclid, and Archimedes.

Pythagoras, of course, is known for the Pythagorean Theorem, which is still used today to find the length of the sides of a right triangle. Euclid, on the other hand, is known for his work in geometry, and he wrote a book called "Elements" that is still used today as a textbook in many math classes. And Archimedes? This guy was a true mathematical genius. He made huge contributions to geometry and calculus, and he even developed a system for calculating the volume of irregularly shaped objects.

Who invented math? Any discussion of the history of math must include the ancient Greeks.

So, who invented math? Not exactly the Greeks, but they deserve tons of credit for advancing the field to entirely new levels.

While the roots of math all stem from ancient civilizations, the history of math continues well beyond ancient times.

Fast forward to the 17th century, and we have the one and only Sir Isaac Newton. Arguably the most famous and influential mathematician of all time, Newton was a true math and science pioneer, and he's responsible for developing the field of calculus. He also made huge contributions to physics and astronomy, so he's basically a superhero in the world of math and science.

Who invented math? Not Sir Isaac Newton—but he is viewed by many as the most influential mathematician of all time.

And let's not forget about another 17th century math legend: Gottfried Leibniz. He also independently developed calculus, which was pretty impressive considering he and Newton were working on opposite sides of Europe at the time. Leibniz was also a philosopher, and he made important contributions to the study of the concept of infinity.

And while this tour through the history of math has so far featured only male mathematicians, there have been tons of incredible contributions made to the field of mathematics by famous women mathematicians like Sophie Germain, Emmy Noether, Katherine Johnson, and Valerie Thomas.

Who invented math? Not Valerie Thomas, but she did use math to invent the illusion transmitter—a 3D imaging technology that was the first of its kind when it was first put into use by NASA in 1980.

In addition to famous women mathematicians, the history of math is filled with contributions made by often overlooked African American mathematicians like Fern Hunt, Mark Dean, and Lonnie Johnson, all of whom played a significant role in the progression of the field.

So, now that you have a better idea of the history of math and how it has developed over thousands of years, can you confidently state who invented math?

The answer should be no. Why? Because mathematics has been around for nearly as long as humanity has had a presence on Earth, and it has evolved by leaps and bounds over thousands of years.

History of Math: Math was discovered and developed by many different cultures and individuals throughout history.

The only way to answer the question “who invented math?“ is to say that math was discovered and developed by many different cultures and individuals throughout history. From the Babylonians to the Greeks to Newton and Leibniz, math has been molded and shaped by countless brilliant minds over the centuries.

In conclusion, mathematics is beautiful and complex field of study, and we owe many men and women gratitude and respect for its development and progression. So, the next time you're struggling through a math problem, just remember that you're a part of a long history of individuals who have been using and refining mathematics for thousands and thousands of years.

Do you want more insights from great mathematicians from history? Click here to see of collection of the 37 Greatest Math Quotes of All Time

---

More Math Resources You Will Love:

Hooda Math—Games, Features, and Benefits

Hooda Math—Games, Features, and Benefits

How Students Can Access Hooda Math Escape Games and Features to Learn Math in a Fun and Engaging Way

Students use games like Hooda Math Escape to practice their math and logic skills.

Hooda Math is an online website that offers a large range of educational puzzles, games, and learning activities for students. The site was founded in 2008 by Michael Edlavitch, a former math teacher who saw the need for a more engaging and interactive way for students to learn math.

Hooda Math has become a popular resource for teachers, parents, and students who are looking for fun and effective ways to improve their math skills. In this blog post, we will explore the features of Hooda Math, how it works, and its benefits.

Features of Hooda Math

Hooda Math offers a wide variety of math games—including the popular Hooda Math Escape Games—and activities that cover a range of topics such as adding, subtracting, multiplying, dividing, working with fractions and decimals, algebra skills, geometry skills, and logical thinking. The website has games that are suitable for math students of all ages and skill levels.

One of the unique features of Hooda Math is that the website offers games that are not only fun, but also educational. The Hooda Math games are designed to help students of all grade levels to improve their math skills by providing them with opportunities to practice and apply what they have learned in class in a gamified setting.

Hooda Math Games ((Image Source: hoodamath.com)

Another great feature of Hooda Math is that it offers a variety of game modes to cater to different learning styles. For example, some games are designed to be played individually, while others can be played collaboratively with others—including friends and classmates. Additionally, some games are timed, while others are not, giving children the opportunity to practice at a comfortable pace.

Hooda Math offers games that are not only fun, but also educational and 100% free.

Hood Math Escape Games

One of the most popular activities on the website are the Hooda Math Escape Games, where players are tasked with escaping a given area, such as New York City, by exploring, collecting items, and solving puzzles along the way.

The Hooda Math escape games often feature a range of challenges, such as finding hidden objects, using logic to solve puzzles, and interacting with the environment to find clues. Players must use their problem-solving skills and creativity to progress through the game and ultimately escape the room or scenario.

Hooda Math Escape Games are available to play for free on their website, and there are many different scenarios and themes to choose from, including escape rooms, schools, zoos, and more. These games can be a fun and challenging way to exercise your brain and test your problem-solving skills.

Hooda Math Escape: Screenshot

Escape Games Hooda Math: Screenshot

How Hooda Math Works

Hooda Math is a free-to-use website that is easy to navigate. Once you arrive on the homepage, you will see a list of games arranged by topic. You can either select a game from the list or use the search bar to find a specific game.

Once you have selected a game, you will be taken to the game's webpage, where you can read instructions on how to play the game. Each game includes a walkthrough tutorial that will show you how to play the game if you need support. Most games on Hooda Math are designed to be played using a keyboard and mouse, but some can also be played on touch-enabled devices like tablets and smartphones.

As you play a Hooda Math game, you will be given tasks to complete, such as solving math problems or answering quiz questions. You will earn points for completing tasks, and your progress will be tracked throughout your playtime. At the end of the game, players will typically be given a score based on how well they performed.

In addition to the escape games, Hooda Math offers games on a variety of math topics including logic and geometry. ((Image Source: hoodamath.com)

Benefits of Hooda Math

Hooda Math offers a range of benefits for students who use it to improve their logic, math, and critical thinking skills. Some of these benefits include:

• Improved Math Skills: Hooda Math provides children with a fun and engaging way to practice math. The games are designed to help children understand and apply math concepts more easily.

• Increased Confidence: As children play games on Hooda Math and see their scores improve, they become more confident in their math abilities. This confidence can translate into better performance in the classroom.

• Personalized Learning: Hooda Math offers games that cater to different learning styles. Children can practice at their own pace and choose games that are suited to their skill level.

• Accessibility: Hooda Math is a free-to-use website that can be accessed from anywhere with an internet connection. This makes it an accessible resource for children who may not have access to other educational materials.

• Engaging and Fun: The games on Hooda Math are designed to be both educational and fun. Children are more likely to engage with educational materials that are entertaining and enjoyable.

The Hooda Math Duck Life games—where you play as a racing duck—are very popular with young students.

Should You Use Hooda Math with Your Students?

Yes! Hooda Math is a valuable free resource for students who are looking for a fun and engaging way to practice math. The website's wide range of games and activities cater to different learning styles and skill levels, making it a versatile tool for improving math skills.

We recommend allowing your students to have access to playing Hooda Math games as a reward for completing classwork early.

You can visit the Hooda Math website and access all of their games and activities by clicking here.

---

More Math Resources You Will Love:

How to Boost Student Engagement with Math Pictures

How to Boost Student Engagement with Math Pictures

Teachers can us math pictures to spark deep discussions and make mathematics more visually accessible for students

Math Pictures can be used to spark student interest and discussion for a variety of topics.

Mathematics is a visual subject, and math pictures are an important tool for understanding and communicating mathematical ideas. Math pictures help us see patterns, visualize concepts, and explore relationships.

In this post, we will explore the world of math pictures in several forms including:

• Graphs and Diagrams

• Think-Notice-Wonder Math Graphics

• Mathematical Art and Visualizations

• Topic-Specific Math Pictures

Math Pictures: Graphs and Diagrams

Graphs and diagrams are perhaps the most common type of pictures for math applications. These visual aids are used to represent real-world data in a visual way that is easy to understand. Graphs can show relationships between variables, patterns in data, and trends over time. There are many different types of graphs, including line graphs, bar graphs, scatter plots, and pie charts.

Picture Math: Graphs and charts are one of the most common types of visual math representations.

Line graphs are used to show how a variable changes over time or in relation to another variable. For example, a line graph might show how the temperature changes throughout the day, or how the stock price of a company changes over the course of a year. Bar graphs are used to compare different categories of data, such as the sales of different products or the number of students in different grade levels. Scatter plots are used to show how two variables are related to each other, such as the relationship between height and weight. Pie charts are used to show how a whole is divided into parts, such as the percentage of a budget that is spent on different categories.

Diagrams are another type of math pictures that can be used to represent relationships between concepts. Venn diagrams, for example, are used to show how sets overlap or do not overlap. Flowcharts are used to show the steps in a process or algorithm. Tree diagrams are used to show the outcomes of different choices or events.

Pictures of Math: Venn Diagrams

Compare/Contrast Colors

Math Pictures: Think-Notice-Wonder

Encouraging students to write about math facilitates the structuring of their thoughts, utilization of crucial terminology, and effective mathematical communication, ultimately resulting in a profound and significant comprehension of the subject.

When you look at this math picture, what do you think? What do you notice? What do you wonder?

A recent trend in math education is the use of captivating think-notice-wonder (TNW) writing prompts to spark student thinking and participation.

TNW activities involve presenting students with a math picture along with a prompt to complete the following statements in writing:

• I Think…

• I Notice…

• I Wonder…

You can learn more about using TNW activities in your classroom by clicking here.

Math Pictures: Think-Notice-Wonder Writing Prompts

Math Pictures: Art and Visualizations

Mathematical art combines the beauty of art with the precision of mathematics. One incredible example of mathematical art are Lissajous figures that are made using a Harmonograph—a mechanical device that uses a pendulum to draw a geometric math picture. Some of the most beautiful Lissajous figures can be found out the Exploratorium Museum in San Francisco, California, where several works by Ivan Moscovich are on display.

Math Pictures: Harmonographs

Math Pictures: Harmonographs

Math Pictures: Harmonographs

Another example of art-related pictures for math learning are Escher tessellations, which are repeating patterns that are created by fitting different shapes together in a precise way.

Math Pictures: Escher Tessellations (Digital)

Math Pictures: Escher Tessellations (Tiles)

Mathematical visualizations are yet another type of math picture that is used to help us understand complex mathematical concepts. Visualizations use color, shape, and movement to represent mathematical objects and relationships. They are often used in fields such as physics, computer science, architecture, and engineering to help researchers understand and model complex systems.

Pictures of math: Architecture is a great way to visualize concepts such as lines, angles, space, and symmetry.

San Francisco, CA

Another example of pictures for math visualization is a heat map. Heat maps are used to show how a variable changes over time or space. For example, a heat map might show how the temperature changes throughout a city or how the stock prices of different companies change over the course of a day. Another example is a network diagram, which is used to show how different nodes or points are connected to each other. Network diagrams are used in fields such as social science and computer science to model complex systems of relationships.

Pictures of Math: Weather Heat Maps

Math Pictures: Topic-Specific Examples

Mathematical pictures are not just useful for professionals and researchers; they can also be used to help students understand difficult concepts. In fact, many math teachers use pictures and diagrams to help their students learn math.

For example, a teacher might use a picture of a number line to help students understand how numbers relate to each other. Here a few more ideas for using math pictures to engage students when learning specific topics:

Math Pictures: The common medical pain scale chart is also a number line!

Here are a few more topic-specific examples of math pictures that you can use to engage your students:

Fractions: Fractions can be one of the most challenging topics for students to grasp. Teachers can use various math pictures to give students a visual way to think about fractions and what they represent.

Relating Fractions to Legos

Exploring parts and wholes with avocados.

Percents: Like fractions, percents can be a tricky topic for students and using visual math pictures is a great way to help students think more creatively about percentages.

Math pictures: Percent of Air per Bag of Chips (by Brand)

Probability: Another math topic that can be highly visual and enhanced by the use of math pictures is probability. In this case, using math pictures that utilize fun and interesting scenarios is a great way to spark student engagement and interest in applying their math skills to making predictions about what will happen next.

Using pictures of math to explore probability.

Money: When teaching students about money and spending, using math pictures that bring relatable scenarios to life is a no brainer.

Math Pictures: Bring money scenarios to life with visual aids.

Geometric Shapes: Teachers can also use math pictures to supplement any lesson on 2D and/or 3D-geometric shapes and their properties.

Math Pictures: Geometric Shapes in Art

Math Pictures: Geometric Shapes in Sculpture

There are many places online to search for math pictures including Google Images and free online stock photo galleries such as Unsplash.

Regardless of the source of the math pictures, your students will be enthusiastic and interested in discussing them, as mathematics is present in our surroundings.

---

More Teaching Insights Just for You:

The Platonic Solids Explained

The Platonic Solids Explained

The Incredible History, Meaning, and Beauty of the Platonic Solids

The 5 Platonic Solids.

The platonic solids are incredible, timeless, and fascinating three-dimensional shapes that have been studied and admired by mathematicians and mystics for thousands and thousands of years.

The platonic solids are named after the ancient Greek philosopher Plato, who believed that these sacred geometrical figures represented the fundamental building blocks of our universe.

In this post, we will explore the history and mathematical properties of the 5 Platonic solids, as well as their significance in mathematics, science, religion, and art.

What are the 5 Platonic Solids?

There are five total platonic solids:

• Tetrahedron: 4 faces, 4 points, 6 edges

• Hexahedron: 6 faces, 8 points, 12 edges

• Octahedron: 8 faces, 6 points, 12 edges

• Icosahedron: 20 faces, 12 points, 30 edges

• Dodecahedron: 12 faces, 20 points, 30 edges

The outlines of the five platonic solids.

The History of the Platonic Solids

The history of Platonic solids can be traced back to ancient Greece, where the geometric shapes were first described by Plato in a dialogue entitled Timaeus. His interest in these geometrical figures is why they are called Platonic Solids today.

Plato believed that our universe was comprised up of five elements: earth, air, fire, water, and aether. He associated each element with a different Platonic solid. According to Plato:

• The tetrahedron represents fire.

• The cube represents earth.

• The octahedron represents air.

• The dodecahedron represents aether.

• The icosahedron represents water.

Platonic Solids Elements as described by Plato.

Plato's ideas about the platonic solids and their relationship with our universe have influenced mathematicians, mystics, and astrologists for thousands of years all the way to modern day. Notably, Plato’s writings on the 5 Platonic Solids strongly influenced the famous Roman engineer and architect Vitruvius, who wrote extensively about the use of the Platonic Solids in architectural design, as well as the Islamic scholar Al-Kindi, who dedicated his life to studying the geometrical and mathematical properties of the 5 Platonic Solids.

Platonic Solids Elements: The Platonic Solids are named after the philosopher Plato, who believed that each figure represented one of the 5 elements that make up our universe.

Platonic Solids Sacred Geometry Relationship

Sacred geometry is a term used to describe the belief that certain geometric shapes have spiritual or divine significance. Since the Platonic Solids are believed to represent the 5 elements that make up the universe, they are considered to be a part of sacred geometry.

Furthermore, sacred geometry is often associated with the study of ancient architecture, art, and symbolism, as well as with various mystical and esoteric traditions. Proponents of sacred geometry believe that these shapes and patterns can be found throughout the natural world and can serve as a means of connecting with higher spiritual realms.

The Platonic Solids can be found in sacred geometry.

One of the most striking features of Platonic solids is that they are all regular polyhedra. This means that each face of the solid is a congruent regular polygon, and the vertices of the solid are all congruent (i.e., identical) and equidistant from the center of the solid. In addition, the angles between the faces and the angles between the edges are all the same.

In relation to sacred geometry, the unique and universal mathematical properties of the Platonic Solids is what makes them so special—and, perhaps to some, even divine.

For example, the ratio of the length of an edge to the length of the radius of the circumscribed sphere (i.e., the sphere that passes through all the vertices of the solid) is the same for all Platonic solids. This ratio is known as the "golden ratio" and has been a subject of fascination for mathematicians and artists for centuries.

The 5 Platonic Solids Explained

How many Platonic Solids are there?

There are five platonic solids: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. Let's explore each of these shapes and their properties.

---

Tetrahedron

The tetrahedron is the simplest platonic solid, consisting of four equilateral triangles that meet at four vertices. Each vertex is surrounded by three other vertices, and the angles between the edges that meet at a vertex are all equal. The tetrahedron has the smallest number of faces, edges, and vertices of all the platonic solids.

---

Cube

The cube is probably the most well-known of the platonic solids, consisting of six square faces that meet at eight vertices. Each vertex is surrounded by three other vertices, and the angles between the edges that meet at a vertex are all right angles. The cube has a total of twelve edges, and each edge is the same length.

---

Octahedron

The octahedron is a three-dimensional shape made up of eight equilateral triangles that meet at six vertices. Each vertex is surrounded by four other vertices, and the angles between the edges that meet at a vertex are all equal. The octahedron has a total of twelve edges, and each edge is the same length.

---

Dodecahedron

The dodecahedron is a shape made up of twelve regular pentagons that meet at twenty vertices. Each vertex is surrounded by three other vertices, and the angles between the edges that meet at a vertex are all equal. The dodecahedron has a total of thirty edges, and each edge is the same length.

---

Icosahedron

The icosahedron is a three-dimensional shape made up of twenty equilateral triangles that meet at twelve vertices. Each vertex is surrounded by five other vertices, and the angles between the edges that meet at a vertex are all equal. The icosahedron has a total of thirty edges, and each edge is the same length.

---

Is there a new Platonic Solid?

While it is not classified as a Platonic Solid, there is an extremely interesting three-dimensional figure called a Buckyball that has many of the same mystical and structural properties of the Platonic Solids.

A buckyball is a type of fullerene, which is a molecule composed entirely of carbon atoms. Buckyballs are also known as C60 molecules because they are made up of 60 carbon atoms arranged in a spherical shape, like a soccer ball.

The structure of buckyballs was discovered in 1985 by scientists Robert Curl, Harold Kroto, and Richard Smalley, who were awarded the Nobel Prize in Chemistry in 1996 for their work. Buckyballs have unique electronic, optical, and mechanical properties, and they have potential applications in fields such as nanotechnology, materials science, and medicine.

If you have ever walked along the waterfront in San Francisco, California, you have likely seen the famous 25-foot Buckyball sculpture in front of the Exploratorium at Pier 15.

The famous Buckyball sculpture in San Francisco.

The structure of a Buckyball, which has faces comprised of hexagons and pentagons.

---

Conclusion: Platonic Solids

Platonic solids are special because they are a group of five regular, convex polyhedra that have the same number of faces meeting at each vertex, and all faces are congruent regular polygons.

The 5 Platonic Solids have unique mathematical properties, such as their relationship between the number of vertices, edges, and faces, as well as symmetries and interesting geometric properties that have made them the subject of study in various fields.

Additionally, their historical significance, recognized by Plato in his philosophical works, has further contributed to their divine status in the fields of mathematics and sacred geometry.

The properties of Platonic solids have fascinated mathematicians and scientists for thousands of years and continue to be a subject of study and fascination today.

More Math Resources You Will Love:

Tags: platonic solids, 5 platonic solids, elements platonic solids, platonic solids elements, platonic solids sacred geometry, five platonic solids, how many platonic solids are there, what are platonic solids