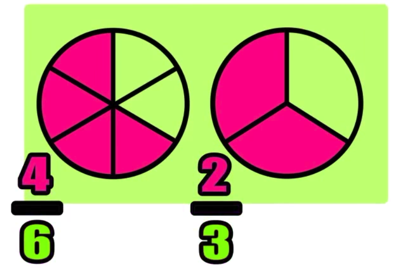
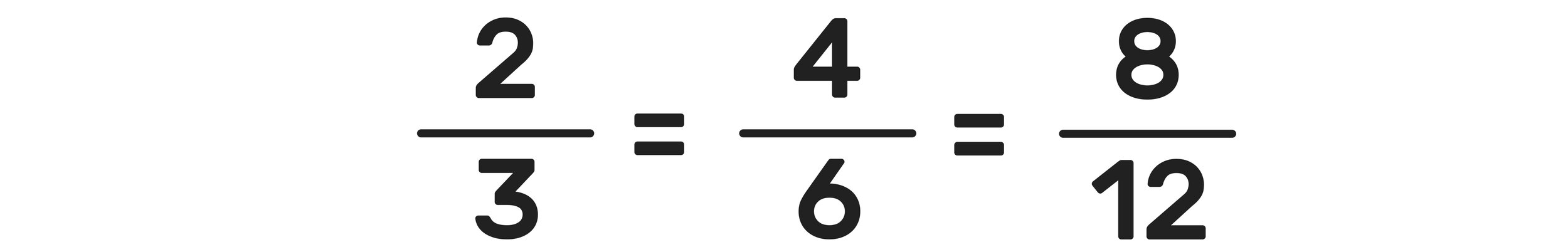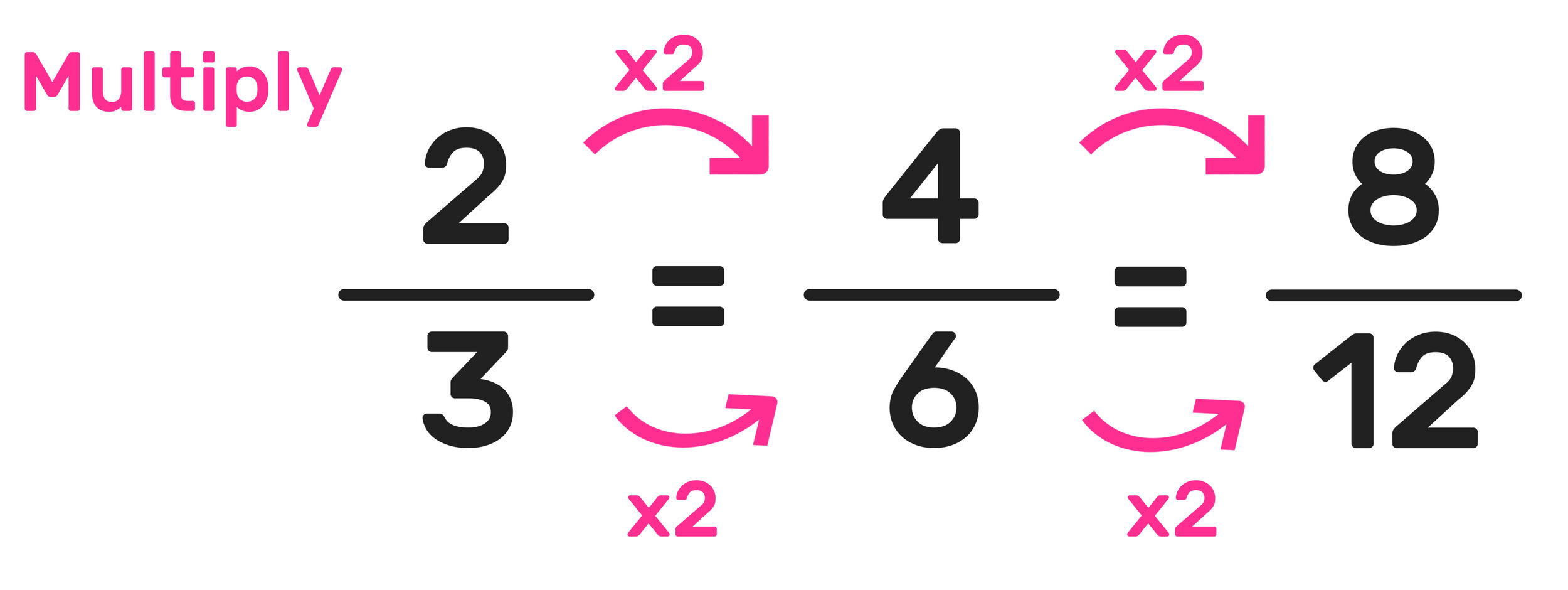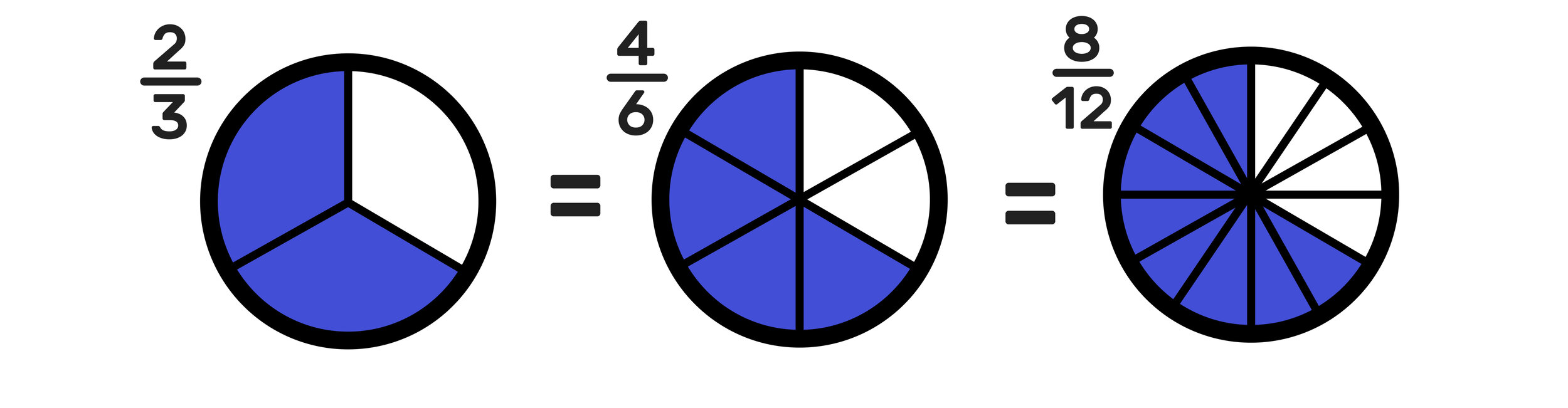Image Source: Mashup Math FP
What is a Hexagon? - Definition, Facts, Examples, and More!
Welcome to this complete guide to hexagons, where you will learn everything you need to know about this beautiful six-sided polygon!
Hexagon Definition:
Source: Mashup Math FP
In mathematics and geometry, a Hexagon is defined as a polygon (a closed two-dimensional shape with straight sides) with 6 sides.
Note that Hexagons have 6 sides and 6 angles.
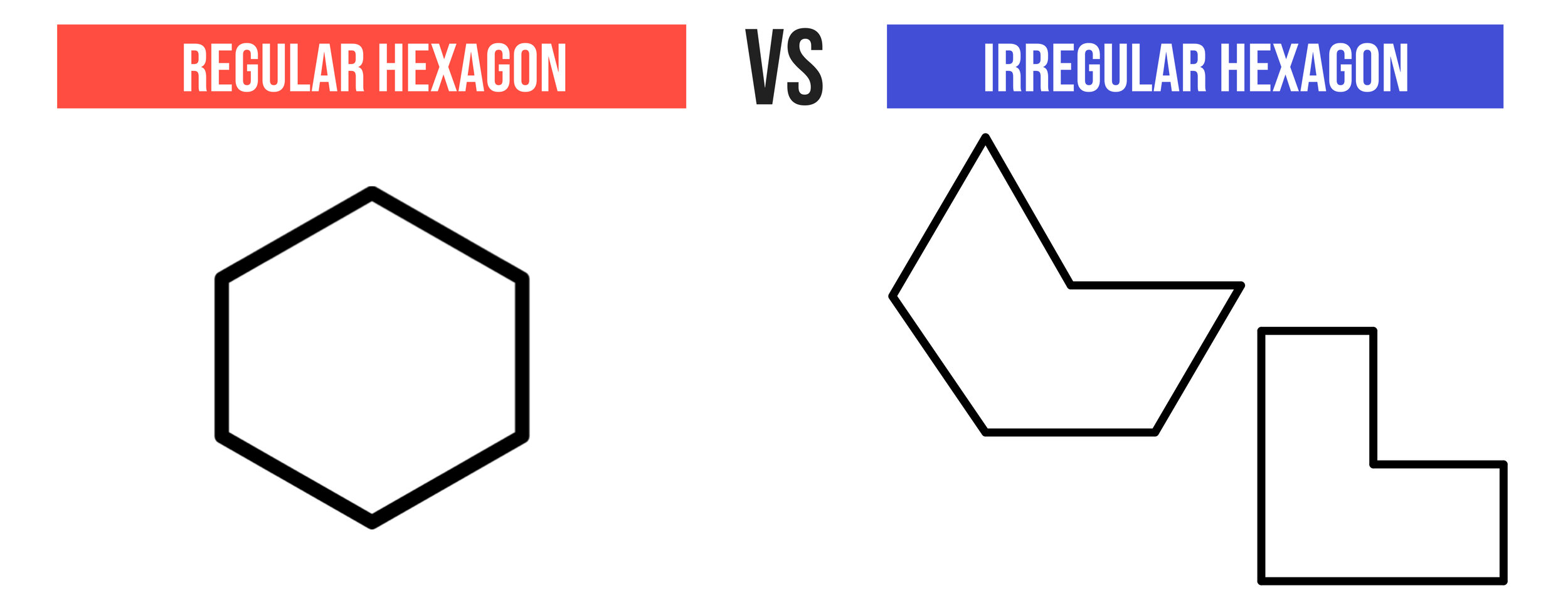
There are two types of Hexagons: Regular Hexagons and Irregular Hexagons.
What is a Regular Hexagon?
A regular hexagon is defined as a 6-sided polygon that is both equilateral and equiangular—meaning that all of the sides have the same length and all of the angles have the same measure.
What is an Irregular Hexagon?
An irregular hexagon is defined as a 6-sided polygon that is not regular—meaning that all of the sides and angles do not have the same measure.
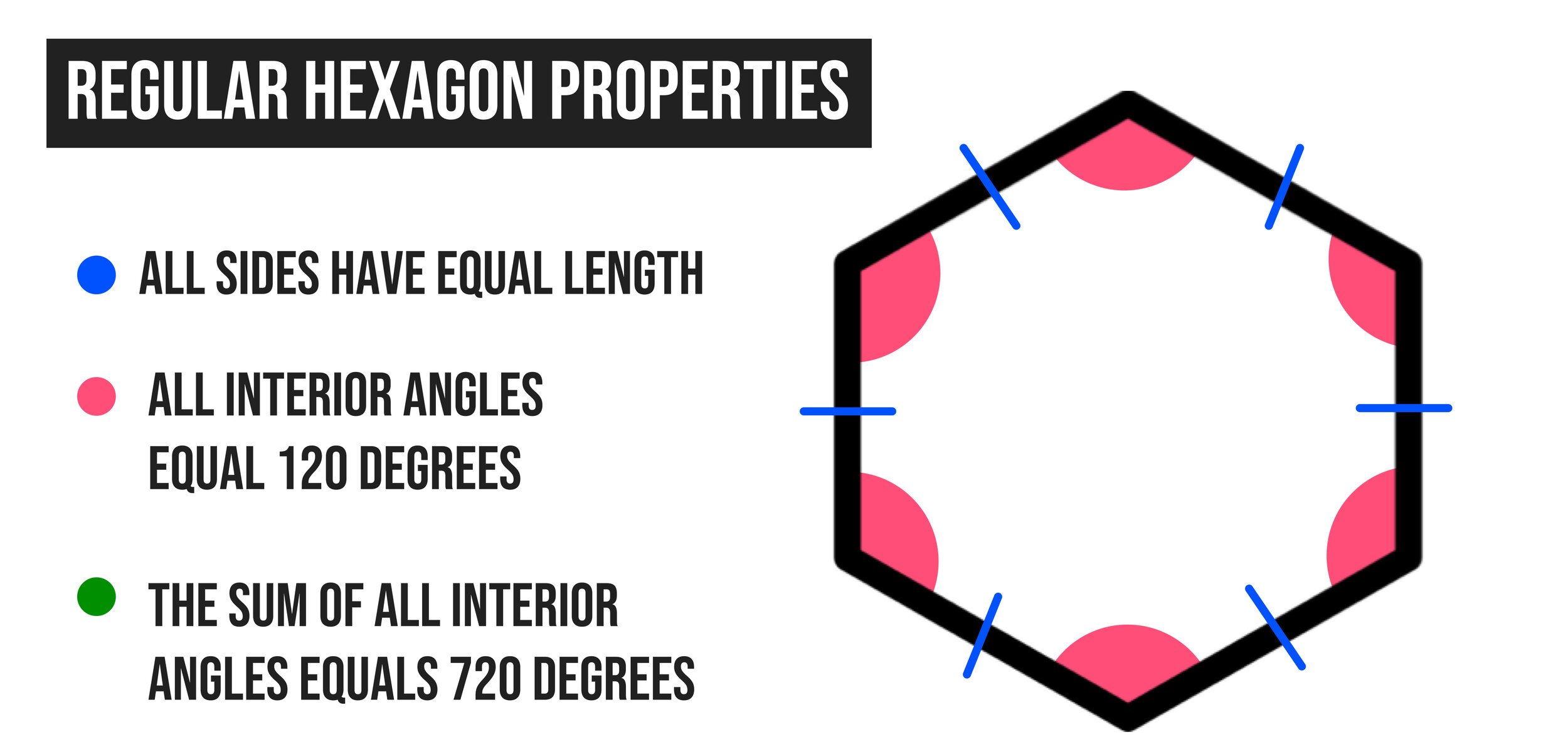
What are the Properties of a Regular Hexagon?
In Geometry, you will most often be dealing with regular hexagons. It is important to know their three main properties:
All sides of a regular hexagon have equal lengths.
All of the interior angles of a regular hexagon are 120° each.
The total sum of the interior angles is 720°.
What Is a 3D Hexagon?
Image via Wikipedia Commons
In Geometry, a 3D Hexagon is called a Hexagonal Prism—which is a prism with hexagonal base.
In the case of 3D hexagons, the hexagonal base is usually a regular hexagon.
For example, a truncated octahedron can be considered a 3D Hexagon because it has a hexagonal base.
Here are a few more examples of 3D Hexagons:
Image Source: Mashup Math FP
Convex Hexagons vs. Concave Hexagons
In Geometry, a polygon is can be convex or concave.
For a hexagon to be convex, all of its interior angles must be less than 180°.
For a hexagon to be concave, at least one of its interior angles must be greater than 180°.
For example, a regular hexagon is also a convex polygon because all of the interior angles equal 120°, which is less than 180°.
Hexagons Degrees: Why 720°?
As previously stated, the measure of each interior angle in a hexagon is 120° and the total sum of all of the interior angles is 720°.
But why? Since there are 6 angles in a regular hexagon and each angle equals 120°, the total sum would be:
120 + 120 + 120 + 120 + 120 + 120 = 720
or
120 x 6 = 720
Furthermore, you can use the polygon interior sum formula to find the sum of the interior angles for any regular polygon.
By applying the polygon interior sum formula to a hexagon, you replace n with 6 (since a hexagon has 6 sides) as follows:
(n - 2) x 180° ➞ (6 - 2) x 180° = 4 x 180° = 720°
Hexagons in Real Life
The hexagon is a simple yet remarkable shape that can be found everywhere and anywhere—ranging from art to architecture to nature. Here a few remarkable examples of hexagons in real life:
Hexagons in Real Life: Snowflakes
Did you know that all snowflakes are hexagons? When ice crystals form, the molecules join together in a hexagonal structure. Mother Nature has determined that this type of formation is the most efficient way for snowflakes to form.
Source: Mashup Math FP
Hexagons in Real Life: Honeycombs
Regular hexagons are one of only three polygons that will tesselate a plane—meaning that they can be duplicated infinitely to fill a space without any gaps. And when bees build honeycombs, they choose to use hexagons. Always!
Mashup Math FP
Hexagons in Real Life: Architecture
Bees are not the only ones who understand the power and efficiency of hexagons. Ancient and modern architecture constantly utilizes this shape from floor tiles to windows to ornate ceiling designs. Hexagons are everywhere!
Photo by Dustin Commer on Unsplash
Hexagons in Real Life: Art
Due to their beautiful form and ability to tessellate, hexagons are constantly used in art and graphic design to create patterns, mosaics, logos, and more!
In fact, many companies choose a hexagon shape for a logo because it represents strength and security.
Source: Mashup Math FP
Hexagons in Real Life: Religion
Since regular hexagons often show up in nature (like snowflakes and honeycombs) they are often included in Sacred Geometry, which assigns higher meaning and spirituality to certain shapes and proportions. In fact, some view the hexagon as the most fascinating shape in relation to the universe.
Source: Mashup Math FP