This free step-by-step guide will teach you everything you need to know about solving systems of equations in math.
Solving Systems of Equations: Everything You Need to Know
Solving systems of equations can seem intimidating, especially when you see more than one equation shown on a graph. However, if you know how to graph a function on the coordinate plane or on a graphing calculator, then you can become a master of solving systems of equations.
This guide also includes a very handy system of equations solver that you can use to check your work and graph linear systems on your computer.
But first…
If you need some refreshers on the foundational skills required to understand how to solve systems of equations, you may find these free algebra resources to be helpful:
You’ll also notice that the graphics in this lesson rely on using different colors to differentiate between different functions (this strategy is very helpful for keeping your thoughts organized and preventing confusion). If you are following along using graph paper, then it is highly recommended that you use colored highlighters or markers. However, this is only a suggestion, and you can still learn to solve systems of equations using a pen or pencil.
Are you ready to get started?
System of Equations Definition
A system of equations is when there are two or more equations that share the same variables.
For example, here is a system of equations for two linear functions:
y = x + 1 & y=-2x + 1
Notice that both of these equations are shown on the graph in Figure 1.
(Again, if you need a refresher on how to graph lines in y=mx+b form, watch this quick video tutorial)
Figure 1 (graph courtesy of desmos.com/calculator)
The solution to a system of equations is the point (or points) where the lines intersect.
So, in this example, the solution to the system of equations is the point (0,1), since this is where the two lines intersect.
Figure 2: What do lightsaber fights and linear systems have in common? (Image: Mashup Math MJ)
Types of Solutions to Systems of Equations
Does every system of equations have a solution?
There are actually three kinds of solutions to a system of equations:
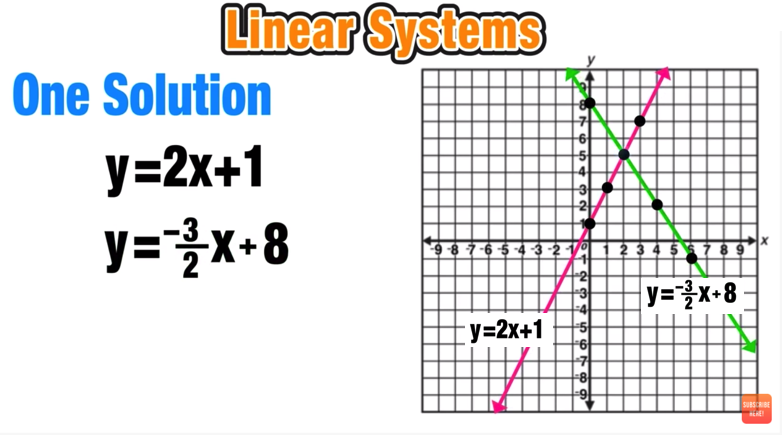
One Solution (as seen in Figure 1)
No Solution
Infinitely Many Solutions
Figure 3
Key Takeaways:
One Solution: The systems intersect at only one point.
No Solution: The lines are parallel and do (and never will) intersect
Infinitely Many Solutions: Two or more identical and overlapping graphs that intersect everywhere!
Confused? That’s ok. Just keep the three solution types in mind as we work through an example of each type of solution that will help you to better understand how to solve systems of linear equations.
Systems of Linear Equations Examples
Example 01: One Solution
Find the solution to the following system of equations:
The first step to finding the solution to this system of equations is to graph both lines as follows:
Notice that the ONLY intersection point for this system of equations is at (2,5).
Remember that (2,5) is an (x,y) coordinate where x=2 and y=5. To confirm that you answer is correct, you can substitute x=2 and y=5 into both equations to see if your answer checks out as follows.
Note that, since this system of equations has only one solution, (2,5) is the only point that will work. You can try substituting x and y values for any other coordinate and you will never find another one that works out.
Final Answer: The solution is (2,5)
Example 02: No Solution
Find the solution to the following system of equations:
Just like the last example, graph both equations on the coordinate plane as follows:
Notice that both equations have the same slope (+5/4). Since parallel lines have the same slope, it makes sense that the lines are the graph are parallel to each other. And, since parallel lines never intersect, these two lines will never intersect, and therefore there is no solution to this system of equations.
Final Answer: No Solution (because the lines are parallel)
Example 03: Infinitely Many Solutions
Find the solution to the following system of equations:
Notice that the second equation is not in y=mx+b form, so you will have to rearrange it to isolate the y before you can graph:
Isolate the y by subtracting 3 from both sides.
What do you notice?
Now we have two equations in our system: y=-4x-3 and… y=-4x-3. After rearranging the second equation, we can see that both equations are identical.
What does this mean for the graph and the solution to our linear system? Let’s find out by graphing the first equation (Figure 5) and then the second equation (Figure 6)
Figure 5
Figure 6
Since the equations are identical, the lines are graphed right on top of each other and they intersect everywhere at every point that both lines pass through.
Therefore, every point on the line is a solution—and since lines have an infinite number of points, this system has an infinite number of solutions.
Final Answer: Infinitely Many Solutions
Systems of Equations Solver
When you initially learn how to solve systems of equations, we recommend using graph paper and a straight-edge to graph your equations and find your solution (and use substitution to check your work as we did in example 01).
However, after you become more comfortable working with systems of equations, you may benefit from using systems of equations solver tool like a graphing calculator to graph lines and find intersection points rapidly.
If you don’t have a graphing calculator, there is an awesome FREE system of equations solver calculator available via www.desmos.com/calculator.
*Note that you have to input the equations in y= form in order for the Desmos systems of equations solver to work.
For example, you can use the Desmos Systems of Equations Solver to find the solution to the system:
y=(3/5)x-8 & y=(-8/5)x+3
1.) Type each equation into the left-hand column
2.) Locate the intersection point (you may need to zoom out)
3.) Click on the intersection point to find the coordinates.
The solution is (5,-5)
Screenshot of Desmos.com/calculator
Systems of Equations Video Lesson
If you are a visual learner and would like to review this step-by-step guide to solving systems of equations as a video tutorial, check out these free tutorials:
Keep Learning with These Free Math Guides:
Share your ideas, questions, and comments below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.